Question

【题目】如图，的面积为.点从点出发，以每秒个单位的速度向点运动:点从点同时出发，以每秒个单位的速度向点运动.规定其中一个点到达端点时，另一个点也随之停止运动。

（1）求线段的长;

（2）设点运动的时间为秒，当时，求的值.

Answer 1

【答案】（1）12 （2）2或3

【解析】

（1）过D作DM⊥AB于M，根据勾股定理求出DM，再根据平行四边形的面积公式求出即可；

（2）①当PC＝BQ时，根据PQ＝BC得出12t＝3t，求出t；

②当PC≠BQ时，过Q作QH⊥DC于H，过B作BN⊥DC于N，求出PH＝CN＝2，得出方程123tt＝2＋2，求出即可．

（1）过D作DM⊥AB于M，

则∠DMA＝90°，

∵∠DAB＝60°，

∴∠ADM＝30°，

∵AD＝4，

∴AM＝AD＝2，DM＝，

∵平行四边形ABCD的面积为24，

∴AB×DM＝24，

∴AB＝12；

（2）根据题意得：DP＝t，BQ＝3t，

①当PC＝BQ时，四边形PCBQ为平行四边形，PQ＝BC，

即12t＝3t，

解得：t＝3；

②当PC≠BQ时，过Q作QH⊥DC于H，过B作BN⊥DC于N，

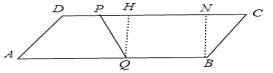
则∠QHN＝∠BNH＝90°，

∵四边形ABCD是平行四边形，

∴∠C＝∠DAB＝60°，∠QHP＝∠BNC＝90°，DC∥AB，

∴∠HQB＝180°∠QHC＝90°，

∴四边形HQBN是矩形，

∴QH＝BN，BQ＝NH＝3t，

在Rt△QHP和Rt△BNC中

∴Rt△QHP≌Rt△BNC（HL），

∴PH＝CN，∠C＝∠QPH＝60°，

∴PH＝PQ＝×4＝2，CN＝BC＝×4＝2，

∴123tt＝2＋2，

解得：t＝2，

综合上述：当PQ＝BC时，t＝2或3．