题目内容
如图,在直角坐标系xOy中,Rt△OAB和Rt△OCD的直角顶点A,C始终在x轴的正半轴上,B,D在第一象限内,点B在直线OD上方,OC=CD,OD=2,M为OD的中点,AB与OD相交于E,当点B位置变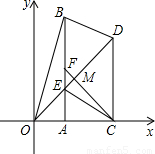 化时,Rt△OAB的面积恒为
化时,Rt△OAB的面积恒为 .
.试解决下列问题:
(1)点D坐标为( );
(2)设点B横坐标为t,请把BD长表示成关于t的函数关系式,并化简;
(3)等式BO=BD能否成立?为什么?
(4)设CM与AB相交于F,当△BDE为直角三角形时,判断四边形BDCF的形状,并证明你的结论.
【答案】分析:(1)在Rt△OCD中,根据勾股定理易求OC=CD=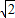 .
.
(2)根据Rt△OAB的面积是 可求出B点的坐标,因为BD2=AC2+(AB-CD)2,所以把B点的坐标代入可得BD长,即可表示成关于t的函数关系式.
可求出B点的坐标,因为BD2=AC2+(AB-CD)2,所以把B点的坐标代入可得BD长,即可表示成关于t的函数关系式.
(3)假设OB=BD,在Rt△OAB中,用t把OB表示出来,根据题(2)中用t表示的BD.两者相等,可得一二次函数表达式,用根的判别式判断是否有解.
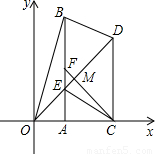
(4)两种情况,先假设∠EBD=90°时(如图2),此时F、E、M三点重合,根据已知条件此时四边形BDCF为直角梯形,然后假设∠EDB=90°时(如图3),根据已知条件,此时四边形BDCF为平行四边形,在Rt△OCD中,OB2=OD2+BD2,用t把各线段表示出来代入,可求出BD=CD= ,即此时四边形BDCF为菱形.
,即此时四边形BDCF为菱形.
解答:解:(1)D( ,
, );(1分)
);(1分)
(2)由Rt△OAB的面积为 ,得B(t,
,得B(t, ),
),
∵BD2=AC2+(AB-CD)2,
∴BD2=( -t)2+(
-t)2+( -
-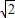 )2=t2+
)2=t2+ -2
-2 (t+
(t+ )+4①
)+4①
= ,
,
∴BD=|t+ ②;
②;
 (3)解法一:若OB=BD,则OB2=BD2.
(3)解法一:若OB=BD,则OB2=BD2.
在Rt△OAB中,OB2=OA2+AB2=t2+ .
.
由①得t2+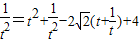 .
.
解得:t+ ,∴t2-
,∴t2- t+1=0,
t+1=0,
∵△= -4=-2<0,∴此方程无解.
-4=-2<0,∴此方程无解.
∴OB≠BD.
解法二:若OB=BD,则B点在OD的中垂线CM上.
∵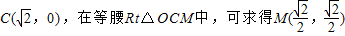 ,
,
∴直线CM的函数关系式为y=-x+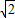 ,③
,③
由Rt△OAB的面积为 .④
.④
联立③,④得:x2-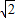 x+1=0,
x+1=0,
∵△=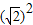 -4=-2<0,∴此方程无解,
-4=-2<0,∴此方程无解,
∴OB≠BD.

解法三:若OB=BD,则B点在OD的中垂线CM上,如图1
过点B作BG⊥y轴于G,CM交y轴于H,
∵S△OBG=S△OAB= ,
,
而S△OMH=S△MOC=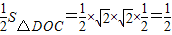 ,(5分)
,(5分)
显然与S△HMO与S△OBG矛盾.
∴OB≠BD.

(4)如果△BDE为直角三角形,因为∠BED=45°,
①当∠EBD=90°时,此时F,E,M三点重合,如图2
∵BF⊥x轴,DC⊥x轴,∴BF∥DC.
∴此时四边形BDCF为直角梯形.
②当∠EDB=90°时,如图3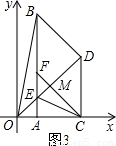
∵CF⊥OD,
∴BD∥CF.
又AB⊥x轴,DC⊥x轴,
∴BF∥DC.
∴此时四边形BDCF为平行四边形.
下证平行四边形BDCF为菱形:
解法一:在△BDO中,OB2=OD2+BD2,
∴t2+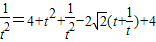 ,
,
∴t+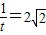 ,
,
[方法①]t2-2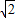 t+1=0,∵BD在OD上方
t+1=0,∵BD在OD上方
解得:t=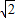 -1,
-1, =
=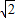 +1或t=
+1或t= +1,
+1, =
=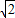 -1(舍去).
-1(舍去).
得 ,
,
[方法②]由②得:BD=t+ ,
,
此时BD=CD= ,
,
∴此时四边形BDCF为菱形(9分)
解法二:在等腰Rt△OAE与等腰Rt△EDB中
∵OA=AE=t,OE= t,则ED=BD=2-
t,则ED=BD=2-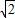 t,
t,
∴AB=AE+BE=t+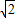 (2-
(2- t)=2
t)=2 -t,
-t,
∴2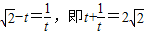 以下同解法一,
以下同解法一,
此时BD=CD= ,
,
∴此时四边形BDCF为菱形.(9分)
点评:此题考查了一次函数解析式的确定、根的判别式、三角形面积的求法、菱形的判定以及勾股定理的应用等知识,综合性强,难度较大.
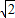 .
.(2)根据Rt△OAB的面积是
 可求出B点的坐标,因为BD2=AC2+(AB-CD)2,所以把B点的坐标代入可得BD长,即可表示成关于t的函数关系式.
可求出B点的坐标,因为BD2=AC2+(AB-CD)2,所以把B点的坐标代入可得BD长,即可表示成关于t的函数关系式.(3)假设OB=BD,在Rt△OAB中,用t把OB表示出来,根据题(2)中用t表示的BD.两者相等,可得一二次函数表达式,用根的判别式判断是否有解.
(4)两种情况,先假设∠EBD=90°时(如图2),此时F、E、M三点重合,根据已知条件此时四边形BDCF为直角梯形,然后假设∠EDB=90°时(如图3),根据已知条件,此时四边形BDCF为平行四边形,在Rt△OCD中,OB2=OD2+BD2,用t把各线段表示出来代入,可求出BD=CD=
 ,即此时四边形BDCF为菱形.
,即此时四边形BDCF为菱形.解答:解:(1)D(
 ,
, );(1分)
);(1分)(2)由Rt△OAB的面积为
 ,得B(t,
,得B(t, ),
),∵BD2=AC2+(AB-CD)2,
∴BD2=(
 -t)2+(
-t)2+( -
-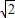 )2=t2+
)2=t2+ -2
-2 (t+
(t+ )+4①
)+4①=
 ,
,∴BD=|t+
 ②;
②; (3)解法一:若OB=BD,则OB2=BD2.
(3)解法一:若OB=BD,则OB2=BD2.在Rt△OAB中,OB2=OA2+AB2=t2+
 .
.由①得t2+
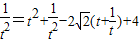 .
.解得:t+
 ,∴t2-
,∴t2- t+1=0,
t+1=0,∵△=
 -4=-2<0,∴此方程无解.
-4=-2<0,∴此方程无解.∴OB≠BD.
解法二:若OB=BD,则B点在OD的中垂线CM上.
∵
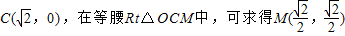 ,
,∴直线CM的函数关系式为y=-x+
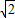 ,③
,③由Rt△OAB的面积为
 .④
.④联立③,④得:x2-
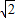 x+1=0,
x+1=0,∵△=
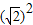 -4=-2<0,∴此方程无解,
-4=-2<0,∴此方程无解,∴OB≠BD.

解法三:若OB=BD,则B点在OD的中垂线CM上,如图1
过点B作BG⊥y轴于G,CM交y轴于H,
∵S△OBG=S△OAB=
 ,
,而S△OMH=S△MOC=
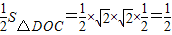 ,(5分)
,(5分)显然与S△HMO与S△OBG矛盾.
∴OB≠BD.

(4)如果△BDE为直角三角形,因为∠BED=45°,
①当∠EBD=90°时,此时F,E,M三点重合,如图2
∵BF⊥x轴,DC⊥x轴,∴BF∥DC.
∴此时四边形BDCF为直角梯形.
②当∠EDB=90°时,如图3

∵CF⊥OD,
∴BD∥CF.
又AB⊥x轴,DC⊥x轴,
∴BF∥DC.
∴此时四边形BDCF为平行四边形.
下证平行四边形BDCF为菱形:
解法一:在△BDO中,OB2=OD2+BD2,
∴t2+
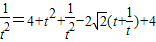 ,
,∴t+
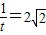 ,
,[方法①]t2-2
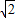 t+1=0,∵BD在OD上方
t+1=0,∵BD在OD上方解得:t=
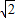 -1,
-1, =
=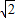 +1或t=
+1或t= +1,
+1, =
=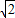 -1(舍去).
-1(舍去).得
 ,
,[方法②]由②得:BD=t+
 ,
,此时BD=CD=
 ,
,∴此时四边形BDCF为菱形(9分)
解法二:在等腰Rt△OAE与等腰Rt△EDB中
∵OA=AE=t,OE=
 t,则ED=BD=2-
t,则ED=BD=2-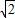 t,
t,∴AB=AE+BE=t+
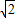 (2-
(2- t)=2
t)=2 -t,
-t,∴2
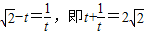 以下同解法一,
以下同解法一,此时BD=CD=
 ,
,∴此时四边形BDCF为菱形.(9分)
点评:此题考查了一次函数解析式的确定、根的判别式、三角形面积的求法、菱形的判定以及勾股定理的应用等知识,综合性强,难度较大.

练习册系列答案
相关题目
 是方程x2-10x+16=0的两个根,且x1<x2,连接MC,过A、B、C三点的抛物线的顶点为N.
是方程x2-10x+16=0的两个根,且x1<x2,连接MC,过A、B、C三点的抛物线的顶点为N.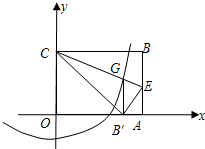 半径的圆与抛物线是否还有除G点以外的交点?若有,请找出这个交点坐标.
半径的圆与抛物线是否还有除G点以外的交点?若有,请找出这个交点坐标. 已如:如图,在直角坐标系中,以y轴上的点C为圆心,2为半径的圆与x轴相切于原点O,AB为⊙C的直径,PA切⊙O于点A,交x轴的负半轴于点P,连接PC交OA于点D.
已如:如图,在直角坐标系中,以y轴上的点C为圆心,2为半径的圆与x轴相切于原点O,AB为⊙C的直径,PA切⊙O于点A,交x轴的负半轴于点P,连接PC交OA于点D. 如图:在直角坐标系中描出A(-4,-4),B(1,-4),C(2,-1),D(-3,-1)四个点.
如图:在直角坐标系中描出A(-4,-4),B(1,-4),C(2,-1),D(-3,-1)四个点.