题目内容
已知抛物线y=ax2+bx+c(a≠0)顶点为C(1,1)且过原点O.过抛物线上一点P(x,y)向直线y=
作垂线,垂足为M,连FM(如图).
(1)求字母a,b,c的值;
(2)在直线x=1上有一点F(1,
),求以PM为底边的等腰三角形PFM的P点的坐标,并证明此时△PFM为正三角形;
(3)对抛物线上任意一点P,是否总存在一点N(1,t),使PM=PN恒成立?若存在请求出t 值,若不存在请说明理由.
值,若不存在请说明理由.
| 5 |
| 4 |
(1)求字母a,b,c的值;
(2)在直线x=1上有一点F(1,
| 3 |
| 4 |
(3)对抛物线上任意一点P,是否总存在一点N(1,t),使PM=PN恒成立?若存在请求出t
 值,若不存在请说明理由.
值,若不存在请说明理由.(1)抛物线y=ax2+bx+c(a≠0)顶点为C(1,1)且过原点O,
可得-
=1,
=1,c=0,
∴a=-1,b=2,c=0.
(2)由(1)知抛物线的解析式为y=-x2+2x,
故设P点的坐标为(m,-m2+2m),则M点的坐标(m,
),
∵△PFM是以PM为底边的等腰三角形
∴PF=MF,即(m-1)2+(-m2+2m-
)2=(m-1)2+(
-
)2
∴-m2+2m-
=
或-m2+2m-
=-
,
①当-m2+2m-
=
时,即-4m2+8m-5=0
∵△=64-80=-16<0
∴此式无解
②当-m2+2m-
=-
时,即m2-2m=-
∴m=1+
或m=1-
Ⅰ、当m=1+
时,P点的坐标为(1+
,
),M点的坐标为(1+
,
)
Ⅱ、当m=1-
时,P点的坐标为(1-
,
),M点的坐标为(1-
,
),
经过计算可知PF=PM,
∴△MPF为正三角形,
∴P点坐标为:(1+
,
)或(1-
,
).
(3)当t=
时,即N与F重合时PM=PN恒成立.
证明:过P作PH与直线x=1的垂线,垂足为H,
在Rt△PNH中,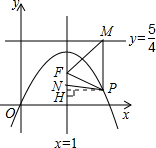
PN2=(x-1)2+(t-y)2=x2-2x+1+t2-2ty+y2,
PM2=(
-y)2=y2-
y+
,
P是抛物线上的点,
∴y=-x2+2x;∴PN2=1-y+t2-2ty+y2=y2-
y+
,
∴-
y+2ty+
-t2=0,y(2t-
)+(
-t2)=0对任意y恒成立.
∴2t-
=0且
-t2=0,
∴t=
,
故t=
时,PM=PN恒成立.
∴存在这样的点.
可得-
| b |
| 2a |
| 4ac-b2 |
| 4a |
∴a=-1,b=2,c=0.
(2)由(1)知抛物线的解析式为y=-x2+2x,
故设P点的坐标为(m,-m2+2m),则M点的坐标(m,
| 5 |
| 4 |
∵△PFM是以PM为底边的等腰三角形
∴PF=MF,即(m-1)2+(-m2+2m-
| 3 |
| 4 |
| 3 |
| 4 |
| 5 |
| 4 |
∴-m2+2m-
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
①当-m2+2m-
| 3 |
| 4 |
| 1 |
| 2 |
∵△=64-80=-16<0
∴此式无解
②当-m2+2m-
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
∴m=1+
| ||
| 2 |
| ||
| 2 |
Ⅰ、当m=1+
| ||
| 2 |
| ||
| 2 |
| 1 |
| 4 |
| ||
| 2 |
| 5 |
| 4 |
Ⅱ、当m=1-
| ||
| 2 |
| ||
| 2 |
| 1 |
| 4 |
| ||
| 2 |
| 5 |
| 4 |
经过计算可知PF=PM,
∴△MPF为正三角形,
∴P点坐标为:(1+
| ||
| 2 |
| 1 |
| 4 |
| ||
| 2 |
| 1 |
| 4 |
(3)当t=
| 3 |
| 4 |
证明:过P作PH与直线x=1的垂线,垂足为H,
在Rt△PNH中,
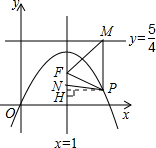
PN2=(x-1)2+(t-y)2=x2-2x+1+t2-2ty+y2,
PM2=(
| 5 |
| 4 |
| 5 |
| 2 |
| 25 |
| 16 |
P是抛物线上的点,
∴y=-x2+2x;∴PN2=1-y+t2-2ty+y2=y2-
| 5 |
| 2 |
| 25 |
| 16 |
∴-
| 3 |
| 2 |
| 9 |
| 16 |
| 3 |
| 2 |
| 9 |
| 16 |
∴2t-
| 3 |
| 2 |
| 9 |
| 16 |
∴t=
| 3 |
| 4 |
故t=
| 3 |
| 4 |
∴存在这样的点.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 ,0),∠ABO=60度.
,0),∠ABO=60度.