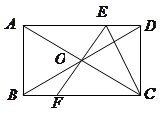
题目内容
已知:如图,梯形ABCD中,AD∥BC,∠ABC=90°.
(1)如图1,若AC⊥BD,且AC=5,BD=3,则S梯形ABCD= ;
(2)如图2,若DE⊥BC于E,BD=BC,F是CD的中点,试问:∠BAF与∠BCD的大小关系如何?请写出你的结论并加以证明;

(3)在(2)的条件下,若AD=EC, = .
= .
(1)如图1,若AC⊥BD,且AC=5,BD=3,则S梯形ABCD= ;
(2)如图2,若DE⊥BC于E,BD=BC,F是CD的中点,试问:∠BAF与∠BCD的大小关系如何?请写出你的结论并加以证明;

(3)在(2)的条件下,若AD=EC,
 = .
= .(1) ;
;
(2)∠BAF=∠BCD.证明如下:
连结EF、BF

∵DF=CF,∠DEC=90°
∴EF=CF= CD
CD
∴∠FEC=∠C
又∠C+∠ADF=180°
∠FEC+∠BEF=180°
∴∠ADF=∠BEF
∵∠BAD=∠ABE=∠BED=90°
∴四边形ABED是矩形
∴AD=BE
∴△ADF≌△FEB
∴FA=FB
∴∠FAB=∠ABF
又BD=BC,DF=CF
∴BF⊥CD
∴∠BFD=∠BAD=90°
∴∠ABF+∠ADF=180°
∴∠ABF=∠C
∴∠BAF=∠BCD
(3)3.
 ;
; (2)∠BAF=∠BCD.证明如下:
连结EF、BF

∵DF=CF,∠DEC=90°
∴EF=CF=
 CD
CD∴∠FEC=∠C
又∠C+∠ADF=180°
∠FEC+∠BEF=180°
∴∠ADF=∠BEF
∵∠BAD=∠ABE=∠BED=90°
∴四边形ABED是矩形
∴AD=BE
∴△ADF≌△FEB
∴FA=FB
∴∠FAB=∠ABF
又BD=BC,DF=CF
∴BF⊥CD
∴∠BFD=∠BAD=90°
∴∠ABF+∠ADF=180°
∴∠ABF=∠C
∴∠BAF=∠BCD
(3)3.
(1)通过平移一腰可知道,梯形的面积可转化为直角三角形的面积,即
连接EF、BF,先证明四边形ABED是矩形,AD=BE,得到△ADF≌△FEB,FA=FB,∠FAB=∠ABF,利用BF⊥CD可证∠ABF=∠C即∠BAF=∠BCD;
(3)利用三角形相似的性质,面积比等于相似比的平方可求解

连接EF、BF,先证明四边形ABED是矩形,AD=BE,得到△ADF≌△FEB,FA=FB,∠FAB=∠ABF,利用BF⊥CD可证∠ABF=∠C即∠BAF=∠BCD;
(3)利用三角形相似的性质,面积比等于相似比的平方可求解

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
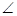 PAB的平分线与
PAB的平分线与

 和19
和19
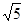 cm,且tan∠EFC=
cm,且tan∠EFC= .
.

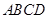 的周长为
的周长为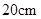 ,两条对角线相交于
,两条对角线相交于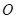 点,过点
点,过点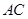 的垂线
的垂线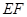 ,分别交
,分别交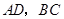 于
于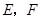 点,连结
点,连结 ,则
,则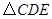 的周长为( )
的周长为( )