题目内容
如图，AP∥BC，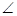
PAB的平分线与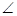CBA的平分线相交于E，CE的延长线交AP于D，
求证：(1)AB=AD+BC(2)若BE=3，AE=4，求四边形ABCD的面积?
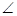PAB的平分线与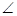CBA的平分线相交于E，CE的延长线交AP于D，求证：(1)AB=AD+BC(2)若BE=3，AE=4，求四边形ABCD的面积?
(1)证明见解析(2)12
延长AE交BC延长线于M
平分
，BE平分
， 
AD//BC 
， 
在
和
中
②由①知：
又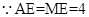
， BE=3
（1）通过构造全等三角形来求解，延长AE交BC的延长线于M；由AP∥BC，及AE平分∠PAB，可求得∠BAE=∠M，即AB=BM，因此直线证得AD=MC即可；在等腰△ABM中，BE是顶角的平分线，根据等腰三角形三线合一的性质知：E是AM的中点，即AE=EM，而PA∥BM，即可证得△ADE≌△MCE，从而得到所求的结论．
（2）由（1）的全等三角形可知：△ADE、△MCE的面积相等，从而将所求四边形的面积转化为等腰△ABM的面积，易得AM、BE的值，从而根据三角形的面积公式求得△ABM的面积，即四边形ADCB的面积．
平分，BE平分 ， AD//BC ， 在和中 ②由①知：
又
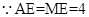， BE=3（1）通过构造全等三角形来求解，延长AE交BC的延长线于M；由AP∥BC，及AE平分∠PAB，可求得∠BAE=∠M，即AB=BM，因此直线证得AD=MC即可；在等腰△ABM中，BE是顶角的平分线，根据等腰三角形三线合一的性质知：E是AM的中点，即AE=EM，而PA∥BM，即可证得△ADE≌△MCE，从而得到所求的结论．
（2）由（1）的全等三角形可知：△ADE、△MCE的面积相等，从而将所求四边形的面积转化为等腰△ABM的面积，易得AM、BE的值，从而根据三角形的面积公式求得△ABM的面积，即四边形ADCB的面积．
练习册系列答案
阅读快车系列答案
相关题目
，高为12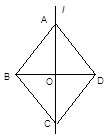
ABCD中，AD=5cm，AB=3cm。AE平分∠BAD交BC于点E，则CE的长等于 （ ）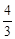
，④
中，正确的有【 】
＝ .