题目内容
如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=5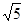 cm,且tan∠EFC=
cm,且tan∠EFC= .
.
(1)△AFB 与△FEC有什么关系? 试证明你的结论。
(2)求矩形ABCD的周长。
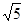 cm,且tan∠EFC=
cm,且tan∠EFC= .
.(1)△AFB 与△FEC有什么关系? 试证明你的结论。
(2)求矩形ABCD的周长。

解:(1)△AFB∽△FEC.
证明:由题意得:∠AFE=∠D=90° 又∠B=∠C=90° ∴∠BAF+∠AFB=90° , ∠EFC+∠AFB=90°
∴∠BAF=∠EFC ∴ AFB∽△FEC
(2)设EC=3x,FC=4x,则有DE="EF=5x" ,∴AB="CD=3x+" 5x=8x
由△AFB∽△FEC得: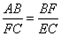 即:
即: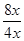 =
=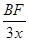 ∴BF=6x ∴BC="BF-CF=6x+" 4x= 10x
∴BF=6x ∴BC="BF-CF=6x+" 4x= 10x
∴在Rt△ADE中,AD=BC=10x,AE=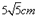 ,则有
,则有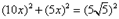
解得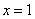 (
(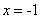 舍去) ∴AB+BC+CD+DA=36x=36(cm) 答:矩形ABCD的周长为36cm.
舍去) ∴AB+BC+CD+DA=36x=36(cm) 答:矩形ABCD的周长为36cm.
证明:由题意得:∠AFE=∠D=90° 又∠B=∠C=90° ∴∠BAF+∠AFB=90° , ∠EFC+∠AFB=90°
∴∠BAF=∠EFC ∴ AFB∽△FEC
(2)设EC=3x,FC=4x,则有DE="EF=5x" ,∴AB="CD=3x+" 5x=8x
由△AFB∽△FEC得:
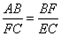 即:
即: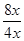 =
=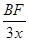 ∴BF=6x ∴BC="BF-CF=6x+" 4x= 10x
∴BF=6x ∴BC="BF-CF=6x+" 4x= 10x∴在Rt△ADE中,AD=BC=10x,AE=
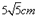 ,则有
,则有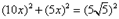
解得
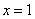 (
(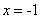 舍去) ∴AB+BC+CD+DA=36x=36(cm) 答:矩形ABCD的周长为36cm.
舍去) ∴AB+BC+CD+DA=36x=36(cm) 答:矩形ABCD的周长为36cm.(1)由四边形BCD是矩形,可得∠AFE=∠D=90°,又由同角的余角相等,可得∠BAF=∠EFC,即可证得:△AFB∽△FEC;
(2)由Rt△FEC中,tan∠EFC= ,可得
,可得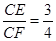 ,则可设CE=3k,则CF=4k,由勾股定理得EF=DE=5k.继而求得BF与BC,则可求得k的值,由矩形ABCD的周长=2(AB+BC)求得结果.
,则可设CE=3k,则CF=4k,由勾股定理得EF=DE=5k.继而求得BF与BC,则可求得k的值,由矩形ABCD的周长=2(AB+BC)求得结果.
(2)由Rt△FEC中,tan∠EFC=
 ,可得
,可得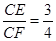 ,则可设CE=3k,则CF=4k,由勾股定理得EF=DE=5k.继而求得BF与BC,则可求得k的值,由矩形ABCD的周长=2(AB+BC)求得结果.
,则可设CE=3k,则CF=4k,由勾股定理得EF=DE=5k.继而求得BF与BC,则可求得k的值,由矩形ABCD的周长=2(AB+BC)求得结果.
练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
 ,④
,④ 中,正确的有【 】
中,正确的有【 】

 = .
= .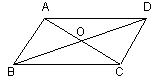



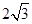
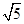




 < S△OQB,若存在,求出t的取值范围,若不存在,试说明理由。
< S△OQB,若存在,求出t的取值范围,若不存在,试说明理由。 