题目内容
图①、图②均为4×4的正方形网格,线段AB、BC的端点均在网点上.按要求在图①、图②中以AB和BC为边各画一个四边形ABCD.
要求:四边形ABCD的顶点D在格点上,且有两个角相等(一组或两组角相等均可);所画的两个四边形不全等.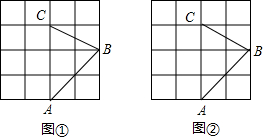
要求:四边形ABCD的顶点D在格点上,且有两个角相等(一组或两组角相等均可);所画的两个四边形不全等.

解:作图如下:
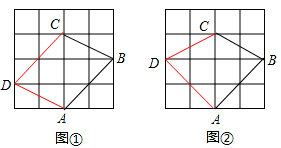

①过C画AB的平行线,过A画BC的平行线,两线交于一点D,根据平行四边形的判定定理可得四边形ABCD是平行四边形,由平行四边形的性质可知∠CBA=∠CDA,∠BAD=∠BCD。
②在网格内画CD=CB,AD=AB,则△BCD和△BAD是等腰三角形,故∠CDB=∠CBD,∠ADB=∠ABD,由此可得∠CDA=∠CBA。
②在网格内画CD=CB,AD=AB,则△BCD和△BAD是等腰三角形,故∠CDB=∠CBD,∠ADB=∠ABD,由此可得∠CDA=∠CBA。

练习册系列答案
相关题目

 ,④
,④ 中,正确的有【 】
中,正确的有【 】
 = .
= .
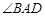 比
比 大
大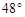 .设
.设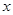 ,
,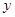 ,那么
,那么
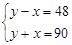
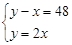
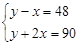
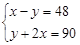
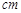 ,BC=26
,BC=26 的速度运动,动点Q从点C开始沿CB以3
的速度运动,动点Q从点C开始沿CB以3 ,问
,问 为何值时,(1)四边形PQCD是平行四边形.(2)当
为何值时,(1)四边形PQCD是平行四边形.(2)当