题目内容
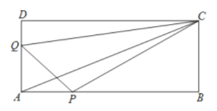
【题目】在长方形ABCD中，AB=3a厘米，BC=a厘米，点P沿AB边从点A开始向终点B以2厘米/秒的速度移动，点Q沿DA边从点D开始向终点A以1厘米/秒的速度移动，如果P、Q同时出发，以t（秒）表示移动的时间，
（1）用含有a、t的代数式表示△APC的面积
（2）求△PQC的面积（用含有a、t的代数式表示）
【答案】（1）at；（2）
或at
【解析】
（1）P的运动距离为△APC的底，高为BC=a不变，将AP用a和t表示出来，再求面积即可.
（2）分两种情况考虑：在点Q到达A前与点Q到达A点后，分别表示出三角形PQC面积即可.
解：(1)由题意得：AP=2t
则S△APC=
=at
（2）①当点Q到达A前：
由题意得：AQ=a-t,高为DC.
则S△AQC=
S△AQP=
所以S△PQC=S△AQC+S△APC-S△AQP
=
+at-（
）
=+at-at+t2
=+t2
②点Q到达A点后
.
综上，△PQC的面积为或at.
练习册系列答案
相关题目
