题目内容
【题目】已知：如图，AM是△ABC的中线，D是线段AM的中点，AM＝AC，AE∥BC．求证：四边形EBCA是等腰梯形．
【答案】见解析.
【解析】
根据三角形判定定理先证明三角形ADE与三角形MDC全等，得出AE=MC=MB，得出四边形AEBM是平行四边形，最后可证明四边形EBCA是等腰梯形．
证明：∵AE∥BC，
∴∠AED＝∠MCD，
∵D是线段AM的中点，
∴AD＝MD，
在△ADE和△MDC中，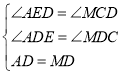
，
∴△ADE≌△MDC（AAS），
∴AE＝MC，
∵AM是△ABC的中线，
∴MB＝MC，
∴AE＝MB，
∵AE∥MB，
∴四边形AEBM是平行四边形，
∴BE＝AM，
∵AM＝AC，
∴BE＝AC，
∵AE∥BC，BE与AC不平行，
∴四边形EBCA是梯形，
∴梯形EBCA是等腰梯形．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
