题目内容
【题目】如图，已知数轴上点A表示的数为8，A是数轴上位于点B右侧的一点，且AB=26动点P从A点出发，每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t>s）秒.
(1)数轴上点B表示的数______点P表示的数______(用含 t 的代数式表示)
(2)若M为AP的中点N为BP的中点，在点P运动的过程中，线段MN的长度是______.
(3)动点Q从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,若点P、Q同时出发，问多少秒时P、Q之间的距离恰好等于2?
(4)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发，问点P运动多少秒时追上点Q?
【答案】（1）-18，8-5t；（2）13；（3）
秒或4秒时P、Q之间的距离恰好等于2；（4）点P运动13秒时追上点Q.
【解析】
（1）根据数轴上的点表示的数右边总比左边的数大及数轴上两点间的距离公式即可得点B表示的数及点P表示的数；（2）分点P在点B左边和右边两种情况，利用数轴上两点间的距离公式可求出BP、AP的长，根据中点的定义可得出PM、PN的长，即可求出MN的长；（3）利用两点间距离公式求出PQ的长即可；（4）分别求出点P、点Q表示的数，根据追上时P、Q表示的数相同即可得答案.
（1）∵A是数轴上位于点B右侧的一点，且AB=26，
∴点B表示的数为8-26=-18，
∵点P从A向左运动，速度为每秒5个单位长度，
∴点P表示的数为：8-5t，
故答案为：-18，8-5t
（2）①如图，当点P在点B右边时，
∵AP=5t，
∴BP=26-5t，
∵M、N分别为AP、BP的中点，
∴PM=
t，PN=
=13-t，
∴MN=PM+PN=t+13-t=13，
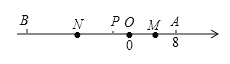
②如图，当点P在点B左边时，
∵AP=5t，
∴BP=5t-26，
∵M、N分别为AP、BP的中点，
∴PM=t，PN=
=t-13，
∴MN=PM-PN=t-(t-13)=13，
综上所述：MN的长为13.
故答案为：13
（3）∵点P从A向左运动，速度为每秒5个单位长度，点Q从B向右运动，速度为2个单位长度，
∴点P表示的数为8-5t，点Q表示的数为-18+2t，
∴PQ=
=2，即
=2，
∴26-7t=2或26-7t=-2，
解得：t=或t=4，
∴秒或4秒时P、Q之间的距离恰好等于2.
（4）∵P、Q都向左运动，速度分别为每秒5个单位长度和3个单位长度，
∴点P表示的数为8-5t，点Q表示的数为-18-3t，
∵点P追上点Q时，P、Q表示的数相同，
∴8-5t=-18-3t，
解得：t=13.
答：点P运动13秒时追上点Q.
