题目内容
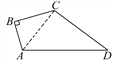
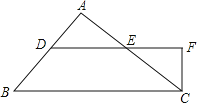
【题目】已知:如图,在△ABC中,∠A=90°,点D、E分别在AB、AC上,DE∥BC,CF与DE的延长线垂直,垂足为F.
(1)求证:∠B=∠ECF ;
(2)若∠B=55°,求∠CED的度数.
【答案】(1)见解析;(2) 145°
【解析】试题分析:(1)先由DE∥BC得出∠B=∠ADE,再根据∠A=90°得出∠ADE+∠AED=90°.由∠F=90°可知∠ECF+∠CEF=90°.由对顶角相等可知∠AED=∠CEF,故∠ADE=∠ECF,由此可得出∠B=∠ECF;
(2)由(1)可知∠B=∠ECF=55°,故∠CED=∠F+∠ECF=90°+55°=145°.
证明:(1)∵DE∥BC,
∴∠B=∠ADE.
∵∠A=90°,
∴∠ADE+∠AED=90°.
∵∠F=90°,
∴∠ECF+∠CEF=90°.
∵∠AED=∠CEF,
∴∠ADE=∠ECF,
∴∠B=∠ECF;
(2)∵由(1)可知∠B=∠ECF=55°,
∴∠CED=∠F+∠ECF=90°+55°=145°.

练习册系列答案
相关题目