题目内容
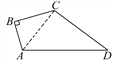
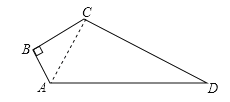
【题目】如图，∠B＝90°，AB＝3，BC＝4，CD＝12，AD＝13.求四边形ABCD的面积．
【答案】36.
【解析】试题分析：连接AC，在直角三角形ABC中，由AB及BC的长，利用勾股定理求出AC的长，再由AD及CD的长，利用勾股定理的逆定理得到三角形ACD为直角三角形，根据四边形ABCD的面积=直角三角形ABC的面积+直角三角形ACD的面积，即可求出四边形的面积．
试题解析：解：连接AC．如图所示：
∵∠B=90°，∴△ABC为直角三角形．又∵AB=3，BC=4，∴根据勾股定理得：AC=
=5．又∵CD=12，AD=13，∴AD2=132=169，CD2+AC2=122+52=144+25=169，∴CD2+AC2=AD2，∴△ACD为直角三角形，∠ACD=90°，则S四边形ABCD=S△ABC+S△ACD=
ABBC+ACCD=×3×4+×5×12=36．
故四边形ABCD的面积是36．
练习册系列答案
名校课堂系列答案
相关题目
【题目】为了深化改革，某校积极开展校本课程建设，计划成立“文学鉴赏”“科学实验”“音乐舞蹈”和“手工编织”等多个社团，要求每位学生都自主选择其中一个社团．为此，随机调查了本校各年级部分学生选择社团的意向，并将调查结果绘制成如下统计图表(不完整)：
某校被调查学生选择社团意向统计表
选择意向 | 文学鉴赏 | 科学实验 | 音乐舞蹈 | 手工编织 | 其他 |
所占百分比 | a | 35% | b | 10% | c |
根据统计图表中的信息，解答下列问题：
(1)求本次调查的学生总人数及a，b，c的值；
(2)将条形统计图补充完整．
