题目内容
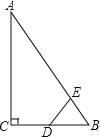
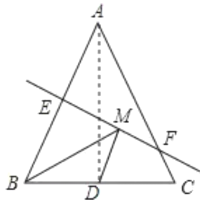
【题目】如图，等腰△ABC底边BC的长为4cm，面积为12cm，腰AB的垂直平分线交AB于点E，若点D为BC边的中点，M为线段EF上一动点，则△BDM的周长最小值为_________
【答案】8cm
【解析】
连接AD，由于△ABC是等腰三角形，点D是BC边的中点，故AD⊥BC，再根据三角形的面积公式求出AD的长，再根据EF是线段AB的垂直平分线可知，点B关于直线EF的对称点为点A，故AD的长为BM＋MD的最小值，由此即可得出结论．
解：如图，连接AD，
∵△ABC是等腰三角形，点D是BC边的中点，
∴AD⊥BC，
∴S△ABC＝
BCAD＝×4×AD＝12，
解得：AD＝6cm，
∵EF是线段AB的垂直平分线，
∴点B关于直线EF的对称点为点A，
∴AD的长为BM＋MD的最小值，
∴△BDM的周长最短＝（BM＋MD）＋BD＝AD＋BC＝6＋×4＝6＋2＝8cm．
故答案为：8cm．
练习册系列答案
相关题目
【题目】为了更好治理河流水质，保护环境，某市治污公司决定购买10台污水处理设备，现有A，B两种型号的设备，其中每台的价格，月处理污水量如表：
A型 | B型 | |
价格（万元/台） | a | b |
处理污水量（吨/月） | 220 | 180 |
经调查：购买一台A型设备比购买一台B型设备多3万元，购买2台A型设备比购买3台B型设备少3万元．
（1）求a，b的值；
（2）经预算：市治污公司购买污水处理设备的资金不超过100万元，你认为该公司有哪几种购买方案；
（3）在（2）问的条件下，若每月要求处理的污水量不低于1880吨，为了节约资金，请你为治污公司设计一种最省钱的购买方案．
