题目内容
【题目】用四块完全相同的小长方形拼成的一个“回形”正方形.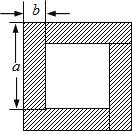
(1)用不同代数式表示图中的阴影部分的面积,你能得到怎样的等式,试用乘法公式说明这个等式成立;
(2)利用(1)中的结论计算:a+b=2,ab=![]() , 求a﹣b;
, 求a﹣b;
(3)根据(1)中的结论,直接写出x+![]() 和x﹣
和x﹣![]() 之间的关系;若x2﹣3x+1=0,分别求出x+
之间的关系;若x2﹣3x+1=0,分别求出x+![]() 和(x﹣
和(x﹣![]() )2的值.
)2的值.
【答案】
(1)
解:阴影部分的面积为:4ab或(a+b)2﹣(a﹣b)2,
得到等式:4ab=(a+b)2﹣(a﹣b)2,
说明:(a+b)2﹣(a﹣b)2=a2+2ab+b2﹣(a2﹣2ab+b2)=a2+2ab+b2﹣a2+2ab﹣b2=4ab.
(2)
解:(a﹣b)2=(a+b)2﹣4ab=2-4×![]() =1,
=1,
∴a-b=![]() 1.
1.
(3)
解:根据(1)中的结论,可得:(x﹣![]() )2=(x+
)2=(x+![]() )2-4,
)2-4,
∵x2﹣3x+1=0,
方程两边都除以x得:![]() ,
,
∴![]() ,
,
∴![]() .
.
【解析】(1)根据阴影部分的面积=4个小长方形的面积=大正方形的面积﹣小正方形的面积,利用完全平方公式,即可解答;
(2)根据完全平方公式解答;
(3)根据完全平分公式解答.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目