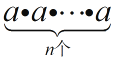ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ‘Ύ«σ1+6+62+63+64+65+66+67+68+69ΒΡ÷Β ±Θ§–ΓΝ÷ΖΔœ÷ΘΚ¥”ΒΎΕΰΗωΦ” ΐΤπΟΩ“ΜΗωΦ” ΐΕΦ ««Α“ΜΗωΦ” ΐΒΡ6±ΕΘ§”Ύ «Υΐ…ηΘΚ
S=1+6+62+63+64+65+66+67+68+69ΔΌ
»ΜΚσ‘ΎΔΌ ΫΒΡΝΫ±ΏΕΦ≥Υ“‘6Θ§ΒΟΘΚ
6S=6+62+63+64+65+66+67+68+69+610ΔΎ
ΔΎ©¹ΔΌΒΟ6S©¹S=610©¹1Θ§Φ¥5S=610©¹1Θ§
Υυ“‘S= ![]() Θ§
Θ§
ΒΟ≥ω¥πΑΗΚσΘ§Α°Ε·Ρ‘ΫνΒΡ–ΓΝ÷œκΘΚ»γΙϊΑ―ΓΑ6Γ±ΜΜ≥…Ή÷ΡΗΓΑaΓ±Θ®aΓΌ0«“aΓΌ1Θ©Θ§ΡήΖώ«σ≥ω1+a+a2+a3+a4+Γ≠+a2014ΒΡ÷ΒΘΩΡψΒΡ¥πΑΗ «Θ®ΓΓΓΓΘ©
A.![]()
B.![]()
C.![]()
D.a2015©¹1
ΓΨ¥πΑΗΓΩB
ΓΨΫβΈωΓΩ…ηS=1+a+a2+a3+a4+Γ≠+a2014 Θ§ ΔΌ
‘ρaS=a+a2+a3+a4+Γ≠+a2014+a2015 Θ§ ΔΎΘ§
ΔΎ©¹ΔΌΒΟΘΚΘ®a©¹1Θ©S=a2015©¹1Θ§
ΓύS= ![]() Θ§
Θ§
Φ¥1+a+a2+a3+a4+Γ≠+a2014= ![]() Θ§
Θ§
Ι ―ΓΘΚBΘ°
ΓΨΩΦΒψΨΪΈωΓΩάϊ”Ο”–άμ ΐΒΡ≥ΥΖΫΚΆΆ§ΒΉ ΐΟίΒΡ≥ΥΖ®Ε‘ΧβΡΩΫχ––≈–ΕœΦ¥Ω…ΒΟΒΫ¥πΑΗΘ§–η“Σ λ÷Σ”–άμ ΐ≥ΥΖΫΒΡΖ®‘ρΘΚ1ΓΔ’ΐ ΐΒΡ»ΈΚΈ¥ΈΟίΕΦ «’ΐ ΐ2ΓΔΗΚ ΐΒΡΤφ¥ΈΟί «ΗΚ ΐΘΜΗΚ ΐΒΡ≈Φ¥ΈΟί «’ΐ ΐΘΜΉΔ“βΘΚΒ±nΈΣ’ΐΤφ ΐ ±: (-a)n=-anΜρ(a -b)n=-(b-a)n , Β±nΈΣ’ΐ≈Φ ΐ ±: (-a)n =an Μρ (a-b)n=(b-a)nΘΜΆ§ΒΉ ΐΟίΒΡ≥ΥΖ®Ζ®‘ρaman=am+n(m,nΕΦ «’ΐ ΐ)Θ°

 –¬ΥΦΈ§ΦΌΤΎΉς“Β νΦΌΦΣΝ÷¥σ―ß≥ωΑφ…γœΒΝ–¥πΑΗ
–¬ΥΦΈ§ΦΌΤΎΉς“Β νΦΌΦΣΝ÷¥σ―ß≥ωΑφ…γœΒΝ–¥πΑΗ άΕΧλΫΧ”ΐ νΦΌ”≈Μ·―ßœΑœΒΝ–¥πΑΗ
άΕΧλΫΧ”ΐ νΦΌ”≈Μ·―ßœΑœΒΝ–¥πΑΗΓΨΧβΡΩΓΩΦΉΘ§““Θ§±ϊΘ§ΕΓΥΡΟϊΧχΗΏ‘ΥΕ·‘±»ϋ«ΑΦΗ¥Έ―ΓΑΈ»ϋ≥…Φ®»γ±μΥυ ΨΘ§ΗυΨί±μ÷–ΒΡ–≈œΔΘ§»γΙϊ“Σ¥”÷–Θ§―Γ‘ώ“ΜΟϊ≥…Φ®ΚΟ”÷ΖΔΜ”Έ»Ε®ΒΡ‘ΥΕ·‘±≤ΈΦ”±»»ϋΘ§Ρ«Ο¥”Π―Γ_____Θ°
ΦΉ | ““ | ±ϊ | ΕΓ | |
ΤΫΨυ ΐΘ®cmΘ© | 185 | 180 | 185 | 180 |
ΖΫ≤ν | 3.6 | 3.6 | 7.9 | 8.2 |