题目内容
【题目】下列条件能判定四边形是平行四边形的是( )
A.一组对边平行,另一组对边相等
B.一组对边平行,一组对角相等
C.一组对边平行,一组邻角互补
D.一组对边相等,一组邻角互补
【答案】B
【解析】解答:解:如图,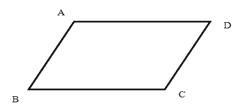
四边形ABCD中,AB∥CD , 此时一组对角相等。
① 若∠A=∠C
AB∥CD , ∠A+∠D=180。
所以∠C+∠D=180,因此BC∥AD
四边形ABCD两组对边分别平行,因此是平行四边形
② 若∠B=∠D
AB∥CD , ∠A+∠D=180
所以∠A+∠B=180,因此BC∥AD
同样为平行四边形
所以答案是:B. 分析:利用平行四边形的判定即可得出.
【考点精析】解答此题的关键在于理解平行四边形的判定的相关知识,掌握两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.

练习册系列答案
相关题目