题目内容
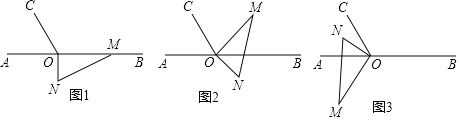
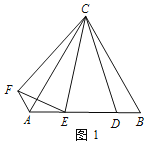
【题目】【操作发现】如图 1，△ABC 为等边三角形，点 D 为 AB 边上的一点，∠DCE=30°，将线段 CD 绕点 C 顺时针旋转 60°得到线段 CF，连接 AF、EF. 请直接 写出下列结果：
① ∠EAF的度数为__________；
② DE与EF之间的数量关系为__________；
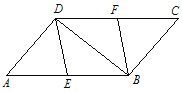
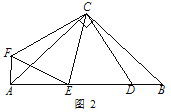
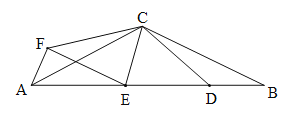
【类比探究】如图 2，△ABC 为等腰直角三角形，∠ACB=90°，点 D 为 AB 边上的一点∠DCE=45°，将线段 CD 绕点 C 顺时针旋转 90°得到线段 CF，连接 AF、EF.
①则∠EAF的度数为__________；
② 线段 AE，ED，DB 之间有什么数量关系？请说明理由；
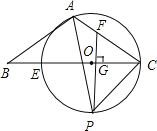
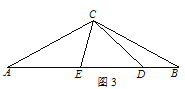
【实际应用】如图 3，△ABC 是一个三角形的余料.小张同学量得∠ACB=120°，AC=BC， 他在边 BC 上取了 D、E 两点，并量得∠BCD=15°、∠DCE=60°，这样 CD、CE 将△
ABC 分成三个小三角形，请求△BCD、△DCE、△ACE 这三个三角形的面积之比.
【答案】 120° DE=EF 90°
【解析】试题分析：（1）①由等边三角形的性质得出AC=BC，∠BAC=∠B=60°，求出∠ACF=∠BCD，证明△ACF≌△BCD，得出∠CAF=∠B=60°，求出∠EAF=∠BAC+∠CAF=120°；
②证出∠DCE=∠FCE，由SAS证明△DCE≌△FCE，得出DE=EF即可；
（2）①由等腰直角三角形的性质得出AC=BC，∠BAC=∠B=45°，证出∠ACF=∠BCD，由SAS证明△ACF≌△BCD，得出∠CAF=∠B=45°，AF=DB，求出∠EAF=∠BAC+∠CAF=90°；
②证出∠DCE=∠FCE，由SAS证明△DCE≌△FCE，得出DE=EF；在Rt△AEF中，由勾股定理得出AE2+AF2=EF2，即可得出结论．
（3）把△BCD绕点C顺时针旋转120°得到△ACF，则可得△ACF≌△BCD，△FCE≌△DEC，得到AF=BD，EF=ED，△AEF是含30°角的直角三角形，S△BCD：S△DCE：S△ACE=BD：ED：AE= AF：EF：AE，即可得到答案．
试题解析：解：（1）①∵△ABC是等边三角形，∴AC=BC，∠BAC=∠B=60°．∵∠DCF=60°，∴∠ACF=∠BCD．在△ACF和△BCD中，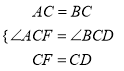 
，∴△ACF≌△BCD（SAS），∴∠CAF=∠B=60°，∴∠EAF=∠BAC+∠CAF=120°；
②DE=EF．理由如下：
∵∠DCF=60°，∠DCE=30°，∴∠FCE=60°﹣30°=30°，∴∠DCE=∠FCE．在△DCE和△FCE中，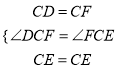 
，∴△DCE≌△FCE（SAS），∴DE=EF；
（2）①∵△ABC是等腰直角三角形，∠ACB=90°，∴AC=BC，∠BAC=∠B=45°．∵∠DCF=90°，∴∠ACF=∠BCD．在△ACF和△BCD中，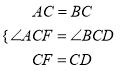 
，∴△ACF≌△BCD（SAS），∴∠CAF=∠B=45°，AF=DB，∴∠EAF=∠BAC+∠CAF=90°；
②AE2+DB2=DE2，理由如下：
∵∠DCF=90°，∠DCE=45°，∴∠FCE=90°﹣45°=45°，∴∠DCE=∠FCE．在△DCE和△FCE中， 
，∴△DCE≌△FCE（SAS），∴DE=EF．在Rt△AEF中，AE2+AF2=EF2．又∵AF=DB，∴AE2+DB2=DE2．
（3）【实际应用】把△BCD绕点C顺时针旋转120°得到△ACF，则△ACF≌△BCD．∵∠ACB=120°，AC=BC ，∴∠B=∠C=30°，∴∠CDE=∠B+∠BCD=30°+15°=45°，∴∠CDB=180°－45°=135°．∵△ACF≌△BCD，∴AE=DB，FC=DC，∠FCA=∠BCD=15°，∠FAC=∠B=30°，∠ACF=∠BDC=135°，∴∠FCE=∠ECD=60°．∵FC=DC，EC=EC，∴△FCE≌△DEC，∴EF=ED，∠CFE=∠CDE=45°，∴∠AFE=135°－45°=90°．∵∠FAE=30°+30°=60°，∴∠AEF=30°，∴AF：EF：AE=1： 
：2，∴S△BCD：S△DCE：S△ACE=BD：ED：AE= AF：EF：AE=1： 
：2．
