题目内容
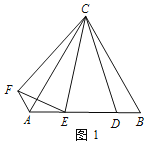
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°,将一直角三角板MON的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
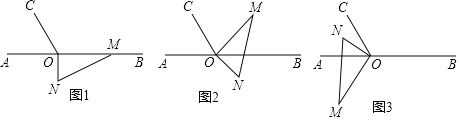
(1)求∠CON的度数;
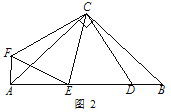
(2)如图2是将图1中的三角板绕点O以每秒10°的速度沿逆时针方向旋转一周的情况.在旋转的过程中,当第t秒时,三条射线OA、OC、OM构成相等的角,求此时t的值;
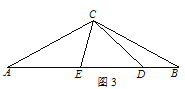
(3)将图1中的三角板绕点O逆时针旋转至图3,使ON在∠AOC的内部时,请探究∠AOM与∠CON的数量关系,并说明理由.
【答案】(1)150°;(2)6或15或24;(3)∠AOM﹣∠CON=30°,理由见解析
【解析】
(1)根据角的和差即可得到结论;
(2)在图2中,要分三种情况讨论:①当∠AOC=∠COM=60°时,②当∠AOM=∠COM=30°时,③当∠AOC=∠AOM=60°时,根据角的和差即可得到结论;
(3)当ON在∠AOC内部时,根据角的和差即可得到结论.
解:(1)由图1可知∠AOC=60°,∠AON=90°,
∴∠CON=∠AOC+∠AON=60°+90°=150°;
(2)在图2中,要分三种情况讨论:
①当∠AOC=∠COM=60°时,此时旋转角∠BOM=60°,
由10°t=60°,解得t=6,
②当∠AOM=∠COM=30°时,此时旋转角∠BOM=150°,
由10°t=150°,解得t=15;
③当∠AOC=∠AOM=60°时,此时旋转角∠BOM=240°,
由10°t=240°,解得t=24.
综上所述,得知t的值为6或15或24;
(3)当ON在∠AOC内部时,∠AOM﹣∠CON=30°,
其理由是:设∠AON=x°,则有∠AOM=∠MON﹣∠AON=(90﹣x)°,
∠CON=∠AOC﹣∠AON=(60﹣x)°,
∴∠AOM﹣∠CON=(90﹣x)°﹣(60﹣x)°=30°.

【题目】某自行车厂一周计划生产![]() 辆自行车,平均每天生产
辆自行车,平均每天生产![]() 辆,由于各种原因实际每天生产量与计划量相比有出入,下表是某周的生产情况(超产为正,减产为负);
辆,由于各种原因实际每天生产量与计划量相比有出入,下表是某周的生产情况(超产为正,减产为负);
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 |
|
|
|
|
|
|
|
![]() 根据记录可知前三天共生产________辆;
根据记录可知前三天共生产________辆;
![]() 产量最多的一天比产量最少的一天多生产________辆;
产量最多的一天比产量最少的一天多生产________辆;
![]() 该厂实行计件工资制,每辆车
该厂实行计件工资制,每辆车![]() 元,超额完成任务每辆奖
元,超额完成任务每辆奖![]() 元,少生产一辆扣
元,少生产一辆扣![]() 元,那么该厂工人这一周的工资总额是多少?
元,那么该厂工人这一周的工资总额是多少?