题目内容
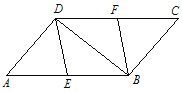
【题目】如图,在□ABCD 中,∠ADB=90°,点 E 为 AB 边的中点,点 F 为CD 边的中点.
(1)求证:四边形 DEBF 是菱形;
(2)当∠A 等于多少度时,四边形 DEBF 是正方形?并说明你的理由.
【答案】见解析
【解析】试题分析:(1)根据平行四边形的性质得出DC∥AB,DC=AB,求出DF∥BE,DF=BE,得出四边形DEBF是平行四边形,求出DE=BE,根据菱形的判定得出即可;
(2)求出AD=BD,根据等腰三角形的性质得出DE⊥AB,根据正方形的判定得出即可.
试题解析:(1)证明:∵四边形ABCD是平行四边形,∴DC∥AB,DC=AB.∵点E为AB边的中点,点F为CD边的中点,∴DF∥BE,DF=BE,∴四边形DEBF是平行四边形.∵∠ADB=90°,点E为AB边的中点,∴DE=BE=AE,∴四边形DEBF是菱形;
(2)当∠A=45°,四边形DEBF是正方形.理由如下:
∵∠ADB=90°,∠A=45°,∴∠A=∠ABD=45°,∴AD=BD.∵E为AB的中点,∴DE⊥AB,即∠DEB=90°.∵四边形DEBF是菱形,∴四边形DEBF是正方形.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目