Question

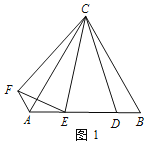
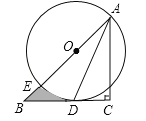
【题目】如图，在△ABC 中，AB=AC，∠BAC=120°，E 为 BC 上一点，以 CE 为直径作⊙O 恰好经过 A、C 两点， PF⊥BC 交 BC 于点 G，交 AC 于点 F．

（1）求证：AB 是⊙O 的切线；

（2）如果 CF =2，CP =3，求⊙O 的直径 EC．

Answer 1

【答案】（1）见解析；（2）⊙O 的直径 EC= 3.

【解析】

（1）若要证明AB是⊙O的切线，则可连接AO，再证明AO⊥AB即可．
（2）连接OP，设OG为x，在直角三角形FCG中，由CF和角ACB为30°，利用30°角所对的直角边等于斜边的一半及勾股定理求出CG的长，即可表示出半径OC和OP的长，在直角三角形CGP中利用勾股定理表示出PG的长，然后在直角三角形OPG中，利用勾股定理列出关于x的方程，求出方程的解即可得到x的值，然后求出直径即可．

证明：（1）连接AO，

∵AB=AC，∠BAC=120°，

∴∠B=∠ACB=30°，

∵AO=CO，

∴∠0AC=∠OCA=30°，

∴∠BAO=120°-30°=90°，

∵OA 是半径

∴AB 是⊙O 的切线；

（2）解：连接OP，

∵PF⊥BC，∴∠FGC=∠EGP=90°，

∵CF=2，∠FCG=30°，∴FG=1，

∴在 Rt△FGC 中 CG=

∵CP=3． ∴Rt△GPC 中，PG=

设 OG=x，则 OC=x+，连接 OP，，显然 OP=OC=x+

在 Rt△OPG 中，由勾股定理知

即(x+)2=x2+()2∴ x .

∴⊙O 的直径 EC=EG+CG=2x++=3.

故答案为：（1）见解析；（2）⊙O 的直径 EC= 3.