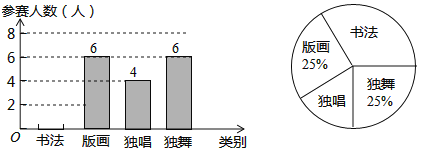
题目内容
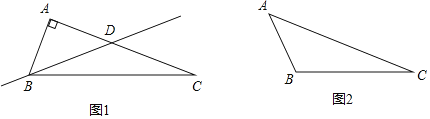
【题目】如图,四边形ABCD是平行四边形,△AB'C和△ABC关于AC所在的直线对称,AD和B'C相交于点O,连接BB'
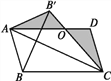
(1)请直接写出图中所有的等腰三角形(不添加字母);
(2)求证:△AB'O≌△CDO
【答案】(1) △ABB',△AOC和△BB'C;(2)证明见解析.
【解析】(1)根据题意,结合图形可知等腰三角形有△ABB′,△AOC和△BB′C;
(2)因为四边形ABCD是平行四边形,所以AB=DC,∠ABC=∠D,又因为,△AB’C和△ABC关于AC所在的直线对称,故AB′=AB,∠ABC=∠AB′C,则可证△AB’O≌△CDO.
解:(1)△ABB',△AOC和△BB'C;
(2)证明:在平行四边形ABCD中,AB=DC,∠ABC=∠D,
由轴对称知AB'=AB,∠ABC=∠AB'C,
∴AB'=CD,∠AB'O=∠D,
在△AB'O和△CDO中,
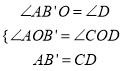 ,
,
∴△AB'O≌△CDO.

练习册系列答案
相关题目