题目内容
【题目】为迎接“国家卫生城市”复检，某市环卫局准备购买A、B两种型号的垃圾箱，通过市场调研得知：购买3个A型垃圾箱和2个B型垃圾箱共需540元；购买2个A型垃圾箱比购买3个B型垃圾箱少用160元．
（1）每个A型垃圾箱和B型垃圾箱各多少元？
（2）现需要购买A，B两种型号的垃圾箱共300个，分别由甲、乙两人进行安装，要求在12天内完成（两人同时进行安装）．已知甲负责A型垃圾箱的安装，每天可以安装15个，乙负责B型垃圾箱的安装，每天可以安装20个，生产厂家表示若购买A型垃圾箱不少于150个时，该型号的产品可以打九折；若购买B型垃圾箱超过150个时，该型号的产品可以打八折，若既能在规定时间内完成任务，费用又最低，应购买A型和B型垃圾箱各多少个？最低费用是多少元？
【答案】(1) A型垃圾箱和B型垃圾箱分别为100元和120元；（2）A型垃圾箱60个，B型垃圾箱240个时，最低费用为29040元．
【解析】分析：（1）设每个A型垃圾箱和B型垃圾箱分别为x元和y元，利用两次购买的费用列方程
，然后解方程组即可；
（2）设购买A型垃圾箱m个，则购买B型垃圾箱（300-m）个，购买垃圾箱的费用为w元，利用工作效率和总工作时间可得到60≤m≤180，然后讨论：若60≤m<150得到w=4m+28800，若150≤m≤180得w=-30m+3600，再利用一次函数的性质求出两种情况下的w的最小值，于是比较大小可得到满足条件的购买方案．
详解：（1）设每个A型垃圾箱和B型垃圾箱分别为x元和y元，
根据题意得,解得
，
∴每个A型垃圾箱和B型垃圾箱分别为100元和120元；
（2）设购买A型垃圾箱m个，则购买B型垃圾箱个，购买垃圾箱的费用为w元，
根据题意得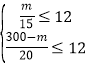
，解得60≤m≤180，
若60≤m＜150，w=100m+120×0.8×=4m+28800，
当m=60时，w最小，w的最小值=4×60+28800=29040（元）；
若150≤m≤180，w=100×0.9×m+120×=﹣30m+36000，
当m=180，w最小，w的最小值=﹣30×180+36000=30600（元）；
∵29040＜30600，
∴购买A型垃圾箱60个，则购买B型垃圾箱240个时，既能在规定时间内完成任务，费用又最低，最低费用为29040元．
小题狂做系列答案
