题目内容
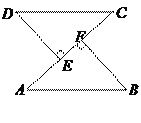
【题目】已知:如图,AB=CD,DE⊥AC,BF⊥AC,E,F是垂足,AE=CF.
求证:(1)DE=BF;(2)AB∥CD.
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:
由AE=CF易得AF=CE,由DE⊥AC,BF⊥AC可得∠AFB=∠CED=90°,结合AB=CD,由“HL”可证得:△ABF≌△CDE,由此可得DE=BF,∠A=∠C,最后可得AB∥CD.
试题解析:
(1)∵AE=CF,
∴AE+EF=CF+EF,即AF=CE,
∵DE⊥AC,BF⊥AC,
∴∠AFB=∠CED=90°,
在Rt△ABF和Rt△CDE中: ![]() ,
,
∴Rt△ABF≌ Rt△CDE,
∴DE=BF.
(2)∵Rt△ABF≌ Rt△CDE,
∴∠A=∠C,
∴AB∥CD.

练习册系列答案
相关题目