题目内容
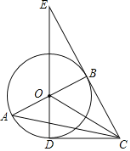
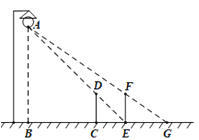
【题目】甲乙两位同学利用灯光下的影子来测量一路灯A的高度,如图,当甲走到点C处时,乙测得甲直立身高CD与其影子长CE正好相等,接着甲沿BC方向继续向前走,走到点E处时,甲直立身高EF的影子恰好是线段EG,并测得EG=2.5m.已知甲直立时的身高为1.75m,求路灯的高AB的长.(结果精确到0.1m)
【答案】路灯高AB约为5.8米.
【解析】试题分析:根据EF⊥BC,CD⊥BC,AB⊥BC,得到AB∥CD∥EF,从而得到△ABN∽△ACD,利用相似三角形对应边的比相等列出比例式求解即可.
解:如图,设AB= x,
由题意知AB⊥BG,CD⊥BG,FE⊥BG,CD=CE,
∴AB∥CD∥EF,∴BE=AB=x,
∴△ABG∽△FEC
∴![]() ,即
,即![]() ,
,
∴![]() m
m
答:路灯高AB约为5.8米.

练习册系列答案
相关题目
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200-2x | |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元[
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.