题目内容
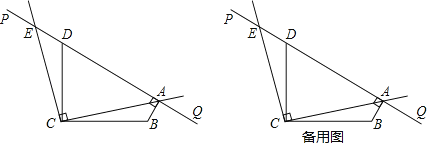
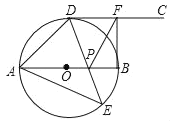
【题目】如图,AB为⊙O的直径,点D、E位于AB两侧的半圆上,射线DC切⊙O于点D,已知点E是半圆弧AB上的动点,点F是射线DC上的动点,连接DE、AE,DE与AB交于点P,再连接FP、FB,且∠AED=45°.
(1)求证:CD![]() AB;
AB;
(2)填空:
①当∠DAE= 时,四边形ADFP是菱形;
②当∠DAE= 时,四边形BFDP是正方形.
【答案】(1)见解析;(2)①![]() ;②90°
;②90°
【解析】
(1)要证明CD∥AB,只要证明∠ODF=∠AOD即可,根据切线的性质,圆周角定理即可证明∠ODF=∠AOD,从而可以解答本题;
(2)①根据四边形ADFP是菱形和菱形的性质,可以求得∠DAE的度数;
②根据四边形BFDP是正方形,可以求得∠DAE的度数.
(1)证明:连接OD,如图所示,
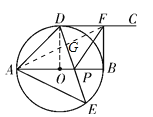
∵射线DC切⊙O于点D,
∴OD⊥CD,
即∠ODF=90°,
∵∠AED=45°,
∴∠AOD=2∠AED=90°,
∴∠ODF=∠AOD,
∴CD∥AB;
(2)①连接AF与DP交于点G,如上图所示,
∵四边形ADFP是菱形,∠AED=45°,OA=OD,
∴AF⊥DP,∠AOD=90°,∠DAG=∠PAG,
∴∠AGE=90°,∠DAO=45°,
∴∠EAG=45°,∠DAG=∠PEG=22.5°,
∴∠EAD=∠DAG+∠EAG=22.5°+45°=67.5°,
故答案为:67.5°;
②∵四边形BFDP是正方形,
∴BF=FD=DP=PB,
∠DPB=∠PBF=∠BFD=∠FDP=90°,
∴此时点P与点O重合,
∴此时DE是直径,
∴∠EAD=90°,
故答案为:90°.

【题目】小张同学尝试运用课堂上学到的方法,自主研究函数y=![]() 的图象与性质.下面是小张同学在研究过程中遇到的几个问题,现由你来完成:
的图象与性质.下面是小张同学在研究过程中遇到的几个问题,现由你来完成:
(1)函数y=![]() 自变量的取值范围是 ;
自变量的取值范围是 ;
(2)下表列出了y与x的几组对应值:
x | … | ﹣2 | ﹣ | m | ﹣ | ﹣ |
|
| 1 |
| 2 | … |
y | … |
|
| 1 |
| 4 | 4 |
| 1 |
|
| … |
表中m的值是 ;
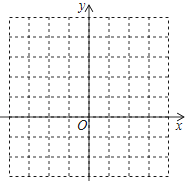
(3)如图,在平面直角坐标系xOy中,描出以表中各组对应值为坐标的点,试由描出的点画出该函数的图象;
(4)结合函数y=![]() 的图象,写出这个函数的性质: .(只需写一个)
的图象,写出这个函数的性质: .(只需写一个)