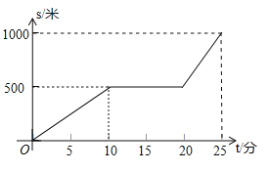
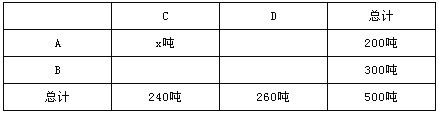
ƒøƒ⁄»›
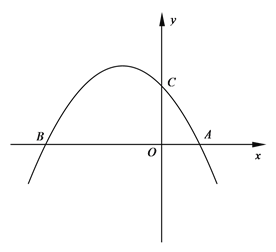
°æƒø°ø»ÁÕº£¨∂˛¥Œ∫Ø ˝y£Ωax2£´2ax£≠3aµƒÕºœÒ”Îx÷·Ωª”⁄A°¢B¡Ωµ„£®µ„A‘⁄µ„Bµƒ”“±fl£©£¨”Îy÷·Ωª”⁄µ„C£Æ
£®1£©«Î÷±Ω”–¥≥ˆA°¢B¡Ωµ„µƒ◊¯±Í£∫A £¨ B £ª
£®2£©»Ù“‘ABŒ™÷±æ∂µƒ‘≤«°∫√æ≠π˝’‚∏ˆ∂˛¥Œ∫Ø ˝ÕºœÒµƒ∂•µ„£Æ
¢Ÿ«Û’‚∏ˆ∂˛¥Œ∫Ø ˝µƒ±Ì¥Ô Ω£ª
¢⁄»ÙPŒ™∂˛¥Œ∫Ø ˝ÕºœÒŒª”⁄µ⁄∂˛œÛœfi≤ø∑÷…œµƒ“ªµ„£¨π˝µ„P◊˜PQ∆Ω––”⁄y÷·£¨Ωª÷±œflBC”⁄µ„Q£Æ¡¨Ω”OQ°¢AQ£¨ «∑ҥʑ⁄“ª∏ˆµ„P£¨ πtan°œOQA£Ω![]() £ø»Áπ˚¥Ê‘⁄£¨«Î«Û≥ˆµ„Pµƒ◊¯±Í£ª»Áπ˚≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
£ø»Áπ˚¥Ê‘⁄£¨«Î«Û≥ˆµ„Pµƒ◊¯±Í£ª»Áπ˚≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
°æ¥∞∏°ø£®1£©A£®1£¨0£©°¢B£®£≠3£¨0£©£ª£®2£©¢Ÿy£Ω£≠![]() x2£≠x£´
x2£≠x£´![]() £ª¢⁄¥Ê‘⁄£¨P£®£≠
£ª¢⁄¥Ê‘⁄£¨P£®£≠![]() £¨
£¨![]() £©
£©
°æΩ‚Œˆ°ø∑÷Œˆ£∫£®1£©¡Óy£Ω0£¨Ω‚πÿ”⁄xµƒ∑Ω≥㨺¥ø…«Û≥ˆA°¢B¡Ωµ„µƒ◊¯±Í£ª
£®2£©¢Ÿ∏˘æ›ABµƒ≥§º∞≈◊œfl∂•µ„◊¯±Íπ´ Ω£¨º¥ø…«Û≥ˆ≈◊ŒÔœflµƒΩ‚Œˆ Ω£ª
¢⁄¿˚”√∫Ø ˝»˝Ω«∫Ø ˝º∞œ‡À∆µƒ≈–∂®”Ζ‘÷ º¥ø…«Û≥ˆ¥∞∏.
œÍΩ‚£∫£®1£©∞—y£Ω0¥˙»Î∂˛¥Œ∫Ø ˝y£Ωax2£´2ax£≠3a£¨
![]() £¨
£¨
°fl![]() £¨
£¨
°‡![]() £¨
£¨
Ω‚µ√£¨![]()
°‡A£®1£¨0£©°¢B£®£≠3£¨0£©£ª
£®2£©¢Ÿ°fl≈◊ŒÔœfl∂•µ„£®£≠1£¨£≠4a£©£¨AB£Ω4£¨
°‡£≠4a£Ω2£¨°‡a£Ω£≠![]() £¨
£¨
°‡y£Ω£≠![]() x2£≠x£´
x2£≠x£´![]() £¨
£¨
¢⁄¥Ê‘⁄“ª∏ˆµ„P£®£≠![]() £¨
£¨![]() £©£¨ πtan°œOQA£Ω
£©£¨ πtan°œOQA£Ω![]() £¨
£¨
°fl![]() £Ω
£Ω![]() £Ω
£Ω![]() £¨
£¨
°‡tan°œABQ£Ω![]() £¨
£¨
°‡°œOQA£Ω°œQBA£¨
°‡°˜AQO°◊°˜ABQ£Æ
°‡AQ2£ΩAO°¡AB£Ω4£¨
…˵„P£®x£¨£≠![]() x2£≠x£´
x2£≠x£´![]() £©£¨‘ÚQ£®x£¨
£©£¨‘ÚQ£®x£¨ ![]() x£´
x£´![]() £©£¨
£©£¨
°‡£®1£≠x£©2£´£®![]() x£´
x£´![]() £©2£Ω4£¨
£©2£Ω4£¨
Ω‚µ√x£Ω£≠![]() ªÚx£Ω1£®≤ª∫œÃ‚“‚£¨…·»•£©£¨
ªÚx£Ω1£®≤ª∫œÃ‚“‚£¨…·»•£©£¨
°‡µ„Pµƒ◊¯±ÍŒ™£®£≠![]() £¨
£¨![]() £©£Æ
£©£Æ

 ‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
‘ƒ∂¡øÏ≥µœµ¡–¥∞∏°æƒø°øƒ≥…Ã≥°œ˙ €![]() °¢
°¢![]() ¡Ω÷÷∆∑≈∆µƒœ¥“¬ª˙£¨Ω¯º€º∞ €º€»Áœ¬±Ì£∫
¡Ω÷÷∆∑≈∆µƒœ¥“¬ª˙£¨Ω¯º€º∞ €º€»Áœ¬±Ì£∫
∆∑≈∆ |
|
|
Ω¯º€£®‘™/ | 1500 | 1800 |
€º€£®‘™/ | 1800 | 2200 |
£®1£©∏√…Ã≥°9‘¬∑›”√45000‘™π∫Ω¯![]() °¢
°¢![]() ¡Ω÷÷∆∑≈∆µƒœ¥“¬ª˙£¨»´≤ø €ÕÍ∫ÛªÒ¿˚9600‘™£¨«Û…Ã≥°9‘¬∑›π∫Ω¯
¡Ω÷÷∆∑≈∆µƒœ¥“¬ª˙£¨»´≤ø €ÕÍ∫ÛªÒ¿˚9600‘™£¨«Û…Ã≥°9‘¬∑›π∫Ω¯![]() °¢
°¢![]() ¡Ω÷÷œ¥“¬ª˙µƒ ˝¡ø£ª
¡Ω÷÷œ¥“¬ª˙µƒ ˝¡ø£ª
£®2£©∏√…Ã≥°10‘¬∑›”÷π∫Ω¯![]() °¢
°¢![]() ¡Ω÷÷∆∑≈∆µƒœ¥“¬ª˙π≤”√»•36000‘™
¡Ω÷÷∆∑≈∆µƒœ¥“¬ª˙π≤”√»•36000‘™
¢ŸŒ ∏√…Ã≥°π≤”–º∏÷÷Ω¯ªı∑Ω∞∏£ø«Îƒ„∞—À˘”–∑Ω∞∏¡–≥ˆ¿¥£ª
¢⁄Õ®π˝º∆À„Àµ√˜œ¥“¬ª˙»´≤øœ˙ €ÕÍ∫Ûƒƒ÷÷Ω¯ªı∑Ω∞∏À˘ªÒµ√µƒ¿˚»Û◊Ó¥Û