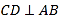Question

【题目】已知，在△ABC中，∠A=90°，AB=AC，点D为BC的中点，∠EDF=90°．

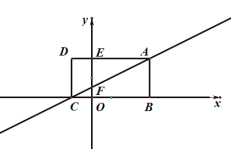
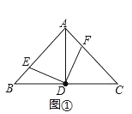
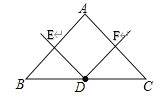
（1）（观察发现）如图①，若点E、F分别为AB、AC上的点，则图中全等三角形一共有 对；

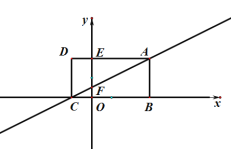
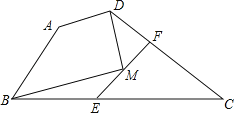
（2）（类比探究）若将∠EDF绕点D在平面内旋转，当旋转到E、F点分别在AB、CA延长线上时，BE=AF吗？请利用图②说明理由．

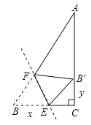
（3）（解决问题）连结EF，把△EDF把绕点D在平面内旋转，当旋转到DF与△ABC的腰所在的直线垂直时，请直接写出∠BDF的度数.

Answer 1

【答案】（1）3；（2）BE=AF；见解析；（3）45°或135°．

【解析】

（1）有3对，即△EDB≌△FDA，△EDA≌△FDC，△ADB≌△ADC.根据等腰三角形的性质可得出AD=BD、∠EBD=∠FAD，根据同角的余角相等可得出∠BDE=∠ADF，由此即可证出△BDE≌△ADF（ASA），其余同理可证得；
（2）根据等腰三角形的性质及等角的补角相等可得出∠EBD=∠FAD、BD=AD，根据同角的余角相等可得出∠BDE=∠ADF，由此即可证出△EDB≌△FDA（ASA），再根据全等三角形的性质即可得出BE=AF．

（3）画出符合条件的图形即可求解.

（1）有3对，即△EDB≌△FDA，△EDA≌△FDC，△ADB≌△ADC.证明如下：

∵AB=AC，点D为BC的中点，

∴∠ADB=∠ADC=90°，BD=CD，

∴△ADB≌△ADC；

∵∠EDB+∠EDA=90°，∠EDA+∠FDA=90°，

∴∠EDB=∠FDA．

在△EDB和△FDA中，，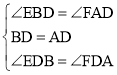

∴△EDB≌△FDA，

同理可证△EDA≌△FDC.

（2）BE=AF，证明如下：

连接AD，如图②所示．

∵∠ABD=∠BAD=45°，

∴∠EBD=∠FAD=135°．

∵∠EDB+∠BDF=90°，∠BDF+∠FDA=90°，

∴∠EDB=∠FDA．

在△EDB和△FDA中，，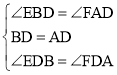

∴△EDB≌△FDA（ASA），

∴BE=AF．

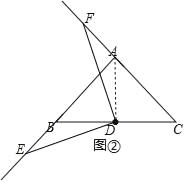
（3）45°或135°．如图所示：

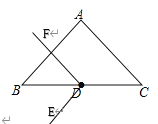
∵DF⊥AC,

∴∠CDF=45°,

∴∠BDF=135°；

或者

∵DF⊥AB,

∴∠BDF=45°；

故答案是：45°或135°．