题目内容
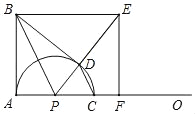
【题目】我们在学习“实数”时画了这样一个图,即“以数轴上的单位长为‘1’的线段作一个正方形,然后以原点O为圆心,正方形的对角线长为半径画弧交数轴于点A”,请根据图形回答下列问题:
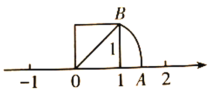
(1)线段OA的长度是多少?(要求写出求解过程)
(2)这个图形的目的是为了说明什么?
(3)这种研究和解决问题的方式体现了 的数学思想方法.(将下列符合的选项序号填在横线上)
A.数形结合 B.代入 C.换元 D.归纳
【答案】(1) OA =![]() ;(2)数轴上的点和实数是一一对应关系;(3)A.
;(2)数轴上的点和实数是一一对应关系;(3)A.
【解析】
(1)首先根据勾股定理求出线段OB的长度,然后结合数轴的知识即可求解;
(2)根据数轴上的点与实数的对应关系即可求解;
(3)本题利用实数与数轴的对应关系即可解答.
解:(1)OB2=12+12=2,
∴OB=![]() ,
,
∴OA=OB=![]()
(2)数轴上的点和实数是一一对应关系
(3) 这种研究和解决问题的方式,体现的数学思想方法是数形结合.
故选A.

练习册系列答案
相关题目
【题目】二次函数y=ax2+bx+c(a、b、c为常数且a≠0)中的x与y的部分对应值如下表:
x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 |
y | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 |
给出了结论:
(1)二次函数y=ax2+bx+c有最小值,最小值为﹣3;
(2)当﹣![]() <x<2时,y<0;
<x<2时,y<0;
(3)a﹣b+c=0;
(4)二次函数y=ax2+bx+c的图象与x轴有两个交点,且它们分别在y轴两侧
则其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4