题目内容
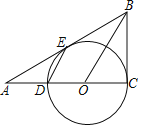
【题目】如图,AB是半圆O的直径,AC是半圆内一条弦,点D是![]() 的中点,DB交AC于点G,过点A作半圆的切线与BD的延长线交于点M,连接AD.点E是AB上的一动点,DE与AC相交于点F.
的中点,DB交AC于点G,过点A作半圆的切线与BD的延长线交于点M,连接AD.点E是AB上的一动点,DE与AC相交于点F.
(1)求证:MD=GD;
(2)填空:①当∠DEA= 时,AF=FG;
②若∠ABD=30°,当∠DEA= 时,四边形DEBC是菱形.

【答案】(1)见解析;(2)①90°;②60°
【解析】
(1)由圆周角定理和切线的性质可得∠M+∠MAD=∠MAD+∠BAD=90°,再结合三角形外角的性质可得∠M=∠AGD,可证AG=AM,由等腰三角形三线合一可得结论;
(2)①由直角三角形的性质可得AF=FG=DF,由等腰三角形的性质和余角的性质可求∠DEA=90°;
②由菱形的性质可得∠DBA=∠DBC=30°,DE∥BC,即可求解.
证明:(1)如图,连接BC.
∵D是![]() 的中点,
的中点,
∴∠DAC=∠ABD,
∵MA是半圆O的切线,
∴MA⊥AB,
∵AB是半圆O的直径,
∴AD⊥DB,
∴∠ADM=90°,
∴∠M+∠MAD=∠MAD+∠BAD=90°,
∴∠M=∠BAD=∠DAC+∠BAG=∠ABD+∠BAG=∠AGD,
∴AG=AM,
∵AD⊥MG,
∴MD=GD;
(2)①若AF=FG,
∵∠ADG=90°,
∴AF=FG=DF,
∴∠DAF=∠ADF,
∴∠ADF=∠ABD,
∵∠ADF+∠EDB=90°,
∴∠ABD+∠EDB=90°,
∴∠DEA=90°,
故答案为:90°;
②若四边形DEBC是菱形,
∴∠DBA=∠DBC=30°,DE∥BC,
∴∠AED=∠ABC=30°+30°=60°,
故答案为:60°.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目