题目内容
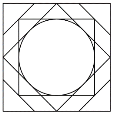
【题目】折纸是一种许多人熟悉的活动.近些年,经过许多人的努力,已经找到了多种将正方形折纸的一边三等分的精确折法,下面探讨其中的一种折法:
(综合与实践)
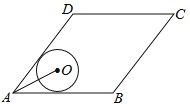
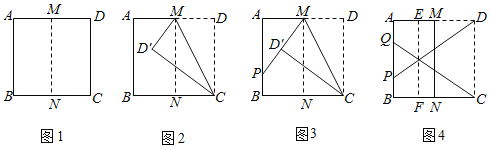
操作一:如图1,将正方形纸片ABCD对折,使点A与点D重合,点B与点C重合,再将正方形纸片ABCD展开,得到折痕MN;
操作二:如图2,将正方形纸片ABCD的右上角沿MC折叠,得到点D的对应的点为D′;
操作三:如图3,将正方形纸片ABCD的左上角沿MD′折叠再展开,折痕MD′与边AB交于点P;
(问题解决)
请在图3中解决下列问题:
(1)求证:BP=D′P;
(2)AP:BP= ;
(拓展探究)
(3)在图3的基础上,将正方形纸片ABCD的左下角沿CD′折叠再展开,折痕CD′与边AB交于点Q.再将正方形纸片ABCD过点D′折叠,使点A落在AD边上,点B落在BC边上,然后再将正方形纸片ABCD展开,折痕EF与边AD交于点E,与边BC交于点F,如图4.试探究:点Q与点E分别是边AB,AD的几等分点?请说明理由.
【答案】(1)见解析;(2)2:1;(3)点Q是AB边的四等分点,点E是AD边的五等分点,理由见解析
【解析】
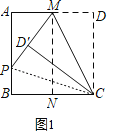
(1)如图1,连接PC,根据正方形的性质、HL定理证明△CD′P≌△CBP,根据全等三角形的性质得出结论;
(2)设BP=x,根据翻转变换的性质、勾股定理列出方程,解方程即可;
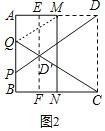
(3)如图2,连接QM,证明Rt△AQM≌Rt△D′QM(HL),得到AQ=D′Q,设正方形ABCD的边长为1,AQ=QD′=y,根据勾股定理列出方程,解方程即可.
(1)证明:如图1,连接PC.
∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=AD,
∴∠MD′C=∠D=90°,
∴∠CD′P=∠B=90°,
在Rt△CD′P和Rt△CBP中,
![]() ,
,
∴Rt△CD′P≌Rt△CBP(HL),
∴BP=D′P;
(2)解:设正方形纸片ABCD的边长为1.则AM=DM=D′M=![]() .
.
设BP=x,则MP=MD′+D′P=DM+BP=![]() +x,AP=1﹣x,
+x,AP=1﹣x,
在Rt△AMP中,根据勾股定理得AM2+AP2=MP2.
∴(![]() )2+(1﹣x)2=(
)2+(1﹣x)2=(![]() +x)2,
+x)2,
解得x=![]() ,
,
∴BP=![]() ,AP=
,AP=![]() ,
,
∴AP:BP=2:1,
故答案为:2:1.
(3)解:点Q是AB边的四等分点,点E是AD边的五等分点.
理由:如图2,连接QM.
∴∠QD′M=180°﹣∠MD′C=90°,
∴∠QD′M=∠A=90°.
在Rt△AQM和Rt△D′QM中,
![]() ,
,
∴Rt△AQM≌Rt△D′QM(HL),
∴AQ=D′Q,
设正方形ABCD的边长为1,AQ=QD′=y,
则QP=AP﹣AQ=![]() ﹣y.
﹣y.
在Rt△QPD′中,根据勾股定理得QD′2+D′P2=QP2.
∵D′P=BP=![]() ,
,
∴y2+(![]() )2=(
)2=(![]() ﹣y)2,
﹣y)2,
解得y=![]() .
.
∴AQ:AB=1:4,即点Q是AB边的四等分点,
∵EF∥AB,
∴![]() ,即
,即 ,
,
解得AE=![]() .
.
∴点E为AD的五等分点.