Question

【题目】如图，已知在Rt△ABC中，∠ACB=90°，AC=8，BC=16，D是AC上的一点，CD=3，点P从B点出发沿射线BC方向以每秒2个单位的速度向右运动.设点P的运动时间为t.连结AP.

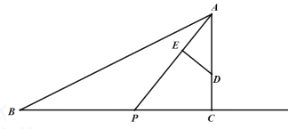
（1）当t=3秒时，求AP的长度(结果保留根号)；

（2）当△ABP为等腰三角形时，求t的值；

（3）过点D做DE⊥AP于点E.在点P的运动过程中，当t为何值时，能使DE=CD？

Answer 1

【答案】（1）AP=；（2）t=或16或5；（3）t=5或11.

【解析】

（1）根据t=3求出BP的长度，进而得到CP的长度，根据勾股定理即可得出答案；

（2）分三种情况进行讨论：①若BA=BP②若AB=AP③若PA=PB分别计算即可得出答案；

（3）分情况进行讨论：①若P在C点的左侧②若P在C点的右侧，根据勾股定理即可得出答案.

（1）当t=3时，BP=6，则CP=10

又∵AC=8

∴AP===

（2）∵BC=16，AC=8

∴BA=

①若BA=BP，则 ；

②若AB=AP，则CP=，BP=32，t=16；

③若PA=PB，则BP=AP=2t，CP=16-2t

在直角三角形ACP中，

，解得：t=5

综上所述：t=或16或5.

（3）分类讨论

∵DE=CD=3，AD=AC-CD=8-3=5

∴AE=4

①若P在C点的左侧，则BP=2t

∴CP=16-2t.

又DE=DC且∠DEP=∠DCP=90°

∴D在∠EPC的角平分线上故PE=PC=16-2t

∴AP=PE+AE=20-2t

则

解得t=5

②若P在C点的右侧，则BP=2t

∴CP=2t-16

又DE=DC且∠DEP=∠DCP=90°

∴D在∠EPC的角平分线上故PE=PC=2t-16

∴AP= PE+AE=2t-12

解得t=11

综上所述：t=5或11.