题目内容
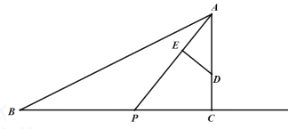
【题目】如图，小明（视为小黑点）站在一个高为10米的高台A上，利用旗杆OM顶部的绳索，划过90°到达与高台A水平距离为17米，高为3米的矮台B.那么小明在荡绳索的过程中离地面的最低点的高度MN是（ ）
A.2米B.2.2米C.2.5米D.2.7米
【答案】A
【解析】
首先得出△AOE≌△DBF（AAS），进而得出CD的长，进而求出OM，MN的长即可．
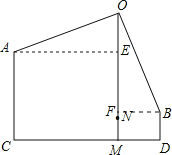
作AE⊥OM，BF⊥OM，
∵∠AOE+∠BOF=∠BOF+∠OBF=90°
∴∠AOE=∠OBF
在△AOE和△DBF中，
∠OEA=∠BFO
∠AOE=∠OBF
OA=OB
∴△AOE≌△DBF（AAS），
∴OE=BF，AE=OF
即OE+OF=AE+BF=CD=17（m）
∵EF=10-3=7
∴OE=5，OF=12
∴OM=OF+FM=15m
由勾股定理得ON=OA=13
∴MN=15-13=2（m）
故答案选择A.
练习册系列答案
相关题目
【题目】某服装店用6000元购进A、B两种新式服装.按照标价出售后获利3800(毛利润=售价-进价)，这两种服装的进价、售价如表所示：
类型 价格 | A型 | B型 |
进价(元/件) | 60 | 100 |
售价(元/件) | 100 | 160 |
(1)求这两种服装各购进的件数：
(2)如果A种服装售价不变，B种服装降价a元出售.这批服装全部售完后所获利润为w.
①写出w与a之间的函数关系式：
②当20≤a≤50时，这批服装全部售出后，获得的最大利润是多少?
