题目内容
【题目】如图所示，一拱桥的截面呈抛物线形状，抛物线两端点与水面的距离都是1m，拱桥的跨度为10m，拱桥与水面的最大距离是5m，桥洞两侧壁上各有一盏距离水面4m景观灯．
（1）求抛物线的解析式；
（2）求两盏景观灯之间的水平距离．
【答案】（1）y=﹣
（x﹣5）2+5（0≤x≤10）；（2）5米．
【解析】试题分析：（1）由图形可知这是一条抛物线，根据图形也可以知道抛物线的顶点坐标为
,与y轴交点坐标是
,设出抛物线的解析式将两点代入可得抛物线方程；
（2）第二题中要求灯的距离，只需要把纵坐标为4代入，求出x，然后两者相减，就是两盏景观灯之间的水平距离．
试题解析：（1）根据题意首先建立坐标系，如图所示：
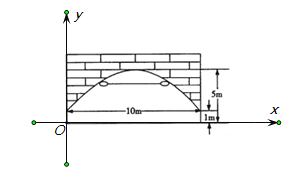
抛物线的顶点坐标为
，与y轴交点坐标是
,
设抛物线的解析式是
把
代入
得
∴
（2）由已知得两景观灯的纵坐标都是4，
∴
∴
∴
∴两景观灯间的距离为
（米）．
练习册系列答案
名校课堂系列答案
相关题目
【题目】为了提高学生书写汉字的能力，增强保护汉字的意识，我市举办了首届“汉字听写大赛”，经选拔后有50名学生参加决赛，这50名学生同时听写50个汉字，若每正确听写出一个汉字得1分，根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表：
组别 | 成绩x分 | 频数（人数） |
第1组 | 25≤x＜30 | 6 |
第2组 | 30≤x＜35 | 8 |
第3组 | 35≤x＜40 | 16 |
第4组 | 40≤x＜45 | a |
第5组 | 45≤x＜50 | 10 |
请结合图表完成下列各题：
（1）求表中a的值；（2）请把频数分布直方图补充完整；
（3）第5组10名同学中，有4名男同学，现将这10名同学平均分成两组进行对抗练习，且4名男同学每组分两人，求小宇与小强两名男同学能分在同一组的概率．
