题目内容
【题目】某商贩出售一批进价为l元的钥匙扣,在销售过程中发现钥匙扣的日销售单价x(元)与日销售量y(个)之间有如下关系:

(1)根据表中数据在平面直角坐标系中,描出实数对(x,y)对应的点;
(2)猜想并确定y与x的关系式,并在直角坐标系中画出x>0时的图像;
(3)设销售钥匙扣的利润为T元,试求出T与x之间的函数关系式:若商贩在钥匙扣售价不超过8元的前提下要获得最大利润,试求销售价x和最大利润T.
【答案】(1)见解析;(2)![]() ,见解析;(3)
,见解析;(3)![]() ,
,![]() ,
,![]() (元).
(元).
【解析】
(1)根据已知各点坐标进而在坐标系中描出即可;
(2)利用各点坐标乘积不变进而得出函数解析式,再画图象;
(3)利用利润=销量×(每件利润),进而得出答案.
解:(1)如图:
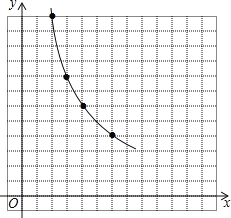
(2)因为各点坐标xy乘积不变,猜想y与x为![]() 形式的反比例函数,
形式的反比例函数,
由题提供数据可知固定k值为24,
所以函数表达式为:![]() ,
,
连线如图:

(3)利润 = 销量 ×(每件利润),
利润为T,销量为y,由(2)知![]() ,
,
每件售价为1,则每件利润为x-1,
所以![]() ,
,
当![]() 最大时,
最大时,![]() 最小,而此时
最小,而此时![]() 最大,
最大,
根据题意,钥匙扣售价不超过8元,
所以![]() 时,
时,![]() (元).
(元).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目