��Ŀ����
����Ŀ�����壺��һ�������������y1��y2������xȡͬһ��ֵ��ʹ��y1��y2����ô��y1��y2Ϊ���������������ƶ�Ӧx��ֵΪy1��y2�ġ������㡱��
�����������������Ϊy1��y2Ϊ����������������ôy1+y2�����ֵ��Ϊy1��y2�ġ���Ӯֵ����
��1���жϺ���y��x+2m��y��![]() �Ƿ�Ϊ������������������ǣ������m��1ʱ���ǵĺ����㣻������ǣ���˵�����ɣ�
�Ƿ�Ϊ������������������ǣ������m��1ʱ���ǵĺ����㣻������ǣ���˵�����ɣ�
��2���жϺ���y��x+2m��y��3x��1��|x|��2���Ƿ�Ϊ������������������ǣ�����������㣻������ǣ���˵�����ɣ�
��3����֪����y��x+2m��y��x2����2m+1��x+��m2+4m��3����0��x��5���ǡ�����������������Ψһ�����㣮
�����m��ȡֵ��Χ��
�������ǵġ���Ӯֵ��Ϊ24�������m��ֵ��
���𰸡���1���� ���������������������㡱Ϊx��2��x����4����2������![]() ��m��
��m��![]() ʱ������y��x+2m��y��3x��1��|x|��2���ǡ���������������m��
ʱ������y��x+2m��y��3x��1��|x|��2���ǡ���������������m��![]() ��m����
��m����![]() ʱ������y��x+2m��y��3x��1��|x|��2�����ǡ���������������3������3��m��1��2��m��6����m��2��
ʱ������y��x+2m��y��3x��1��|x|��2�����ǡ���������������3������3��m��1��2��m��6����m��2��![]() ��m����3+
��m����3+![]() ��
��
��������
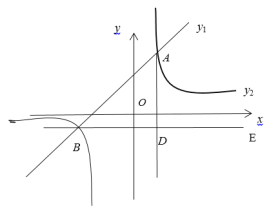
(1)����y��x+2m��y��![]() ��������һ���������ޣ��������������й����㣬�����ж����������ǡ�������������������x+2��
��������һ���������ޣ��������������й����㣬�����ж����������ǡ�������������������x+2��![]() �����x����4��x��2�����������㡱��
�����x����4��x��2�����������㡱��
(2)�����ǡ��������������������㡱Ϊx��m+![]() ������|x|��2���ɵõ���
������|x|��2���ɵõ���![]() ��m��
��m��![]() ʱ���ǡ���������������m��
ʱ���ǡ���������������m��![]() ��m����
��m����![]() ʱ�����ǡ�������������
ʱ�����ǡ�������������
(3)������֪�ɵã�x+2m��x2����2m+1��x+��m2+4m��3�������x��m+3��x��m��1��������֪�ɵõ�0��m+3��5ʱ����3��m��2����0��m��1��5ʱ��1��m��6����Ϊֻ��һ���������㡱��3��m��1��2��m��6����y��x+2m��0��x��5�����ֵΪ5+2m������3��m��1ʱ�������ĶԳ��ᩁ![]() ��m+
��m+![]() ��
��![]() ����ʱ��x��5ʱ�����ֵm2��6m+16����2��m��6ʱ���Գ���
����ʱ��x��5ʱ�����ֵm2��6m+16����2��m��6ʱ���Գ���![]() ��m+
��m+![]() ��
��![]() ����x��0ʱ�����ֵm2+4m��3�����ɡ���Ӯֵ��������mֵ��
����x��0ʱ�����ֵm2+4m��3�����ɡ���Ӯֵ��������mֵ��
�⣻(1)��y��x+2m�Ǿ�����һ����������ֱ�ߣ�y��![]() �Ǿ�����һ����������˫���ߣ�
�Ǿ�����һ����������˫���ߣ�
���������й����㣬
�����xȡͬһ��ֵ��ʹ��y1��y2��
�ຯ��y��x+2m��y��![]() �ǡ�������������
�ǡ�������������
��m��1ʱ��y��x+2��
��x+2��![]() �����x����4��x��2��
�����x����4��x��2��
�ࡰ�����㡱Ϊx��2��x����4��
(2)���躯��y��x+2m��y��3x��1�ǡ�������������
��x+2m��3x��1��
��x��m+![]() ��
��
��|x|��2��
�ੁ2��m+![]() ��2��
��2��
�ੁ![]() ��m��
��m��![]() ��
��
�൱��![]() ��m��
��m��![]() ʱ������y��x+2m��y��3x��1��|x|��2���ǡ���������������m��
ʱ������y��x+2m��y��3x��1��|x|��2���ǡ���������������m��![]() ��m����
��m����![]() ʱ������y��x+2m��y��3x��1��|x|��2�����ǡ�������������
ʱ������y��x+2m��y��3x��1��|x|��2�����ǡ�������������
(3)���ߺ���y��x+2m��y��x2����2m+1��x+��m2+4m��3����0��x��5���ǡ�������������
��x+2m��x2����2m+1��x+��m2+4m��3����
��x2����2m+2��x+��m2+2m��3����0��
��x��m+3��x��m��1��
��0��x��5ʱ��Ψһ�����㣬
��0��m+3��5ʱ����3��m��2��
��0��m��1��5ʱ��1��m��6��
�ੁ3��m��1��2��m��6ʱ���������⣻
��y��x+2m��0��x��5�����ֵΪ5+2m��
y��x2����2m+1��x+��m2+4m��3���ĶԳ���Ϊx��m+![]() ��
��
����3��m��1ʱ����![]() ��m+
��m+![]() ��
��![]() ��
��
��x��5ʱ�����ֵ�����ֵΪm2��6m+16��
��5+2m+m2��6m+17��24��
���m��2+![]() ��m��2��
��m��2��![]() ��
��
��m��2��![]() ��
��
��2��m��6ʱ����![]() ��m+
��m+![]() ��
��![]() ��
��
��x��0ʱ�����ֵ�����ֵΪm2+4m��3��
��5+2m+m2+4m��3��24��
���m����3+![]() ��m����3��
��m����3��![]() ��
��
��m����3+![]() ��
��
����������m��2��![]() ��m����3+
��m����3+![]() ��
��

 ��һ������Ԫͬ�����ؾ�ϵ�д�
��һ������Ԫͬ�����ؾ�ϵ�д�