题目内容
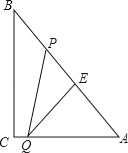
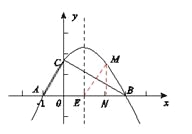
【题目】在平面直角坐标系xoy中, 一块含60°角的三角板作如图摆放,斜边 AB在x轴上,直角顶点C在y轴正半轴上,已知点A(-1,0).

(1)请直接写出点B、C的坐标:B( , )、C( , );并求经过A、B、C三点的抛物
线解析式;
(2)现有与上述三角板完全一样的三角板DEF(其中∠EDF=90°,∠DEF=60°),把顶点E放在线段
AB上(点E是不与A、B两点重合的动点),并使ED所在直线经过点C. 此时,EF所在直线与(1)中的抛物线交于第一象限的点M.
①设AE=x,当x为何值时,△OCE∽△OBC;
②在①的条件下探究:抛物线的对称轴上是否存在点P使△PEM是等腰三角形,若存在,请求点P的坐标;若不存在,请说明理由.
【答案】(1)B(3,0),C(0,![]() ),
),![]() (2)①x=2②存在P点坐标为(1,2)或(1,—2)或(1,2
(2)①x=2②存在P点坐标为(1,2)或(1,—2)或(1,2![]() )或(1,
)或(1,![]() )
)
【解析】
解:(1)B(3,0),C(0,![]() )。
)。
∵A(—1,0)B(3,0)
∴可设过A、B、C三点的抛物线为![]() 。
。
又∵C(0,![]() )在抛物线上,∴
)在抛物线上,∴![]() ,解得
,解得![]() 。
。
∴经过A、B、C三点的抛物线解析式![]() 即
即![]() 。
。
(2)①当△OCE∽△OBC时,则![]() 。
。
∵OC=![]() , OE=AE—AO=x-1, OB=3,∴
, OE=AE—AO=x-1, OB=3,∴![]() 。∴x=2。
。∴x=2。
∴当x=2时,△OCE∽△OBC。
②存在点P。
由①可知x=2,∴OE=1。∴E(1,0)。 此时,△CAE为等边三角形。
∴∠AEC=∠A=60°。
又∵∠CEM=60°, ∴∠MEB=60°。
∴点C与点M关于抛物线的对称轴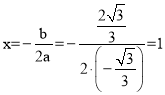 对称。
对称。
∵C(0,![]() ),∴M(2,
),∴M(2,![]() )。
)。
过M作MN⊥x轴于点N(2,0),
∴MN=![]() 。 ∴ EN=1。
。 ∴ EN=1。
∴![]() 。
。
若△PEM为等腰三角形,则:
ⅰ)当EP=EM时, ∵EM=2,且点P在直线x=1上,∴P(1,2)或P(1,-2)。
ⅱ)当EM=PM时,点M在EP的垂直平分线上,∴P(1,2![]() ) 。
) 。
ⅲ)当PE=PM时,点P是线段EM的垂直平分线与直线x=1的交点,∴P(1,![]() )
)
∴综上所述,存在P点坐标为(1,2)或(1,—2)或(1,2![]() )或(1,
)或(1,![]() )时,
)时,
△EPM为等腰三角形。
(1)由已知,根据锐角三角函数定义和特殊角的三角函数值可求出OC和AB的长,从而求得点B、C的坐标。设定交点式,用待定系数法,求得抛物线解析式。
(2)①根据相似三角形的性质,对应边成比例列式求解。
②求得EM的长,分EP=EM, EM=PM和PE=PM三种情况求解即可。

 名校课堂系列答案
名校课堂系列答案