题目内容
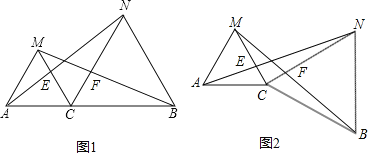
【题目】如图,已知点C是AB上一点,△ACM、△CBN都是等边三角形。
(1)△ACN≌△MCB吗?为什么?
(2)证明:CE=CF;
(3)若△CBN绕着点C旋转一定的角度(如图2),则上述2个结论还成立吗?
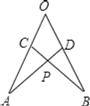
(4)若AN、MB相交于O,则∠AOB度数有没变化?若没有变化,则∠AOB= .
【答案】(1)见解析;(2)见解析;(3)△ACN≌△MCB成立,CE=CF不成立;(4)120°.
【解析】
(1)根据等边三角形性质得出AC=CM,CN=CB,∠ACM=∠BCN=60°,求出∠ACN=∠BCM,根据SAS证出△ACN≌△MCB即可;
(2)因为∠ACB=180°,∠ACM=∠BCN=60°,所以∠MCN=∠BCN,又因为△ACN≌△MCB,所以∠ABM=∠ANC,则可根据ASA判定△CEN≌△CFB,即CE=CF;
(3)由(1)的条件不变,即可证明△ACN≌△MCB成立;由于证明△CEN≌△CFB的条件不够,则CE=CF不成立;
(4)由三角形的外角性质,∠AOB=∠ONB+∠OBN,然后由∠ABM=∠ANC,则∠AOB=∠CNB+∠CBN=120°,即可.
解:(1)∵△ACM与△CBN为等边三角形,
∴∠ACM=∠BCN=60°,AC=MC,BC=NC,
∴∠ACN=∠MCB
∴△ACN≌△MCB(SAS)
(2)∵∠ACB=180°,∠ACM=∠BCN=60°,
∴∠MCN=∠BCN=60°,
∵△ACN≌△MCB,
∴∠ABM=∠ANC,
∵∠MCN=∠BCN,BC=CN,∠ABM=∠ANC,
∴△CEN≌△CFB(ASA),
∴CE=CF
(3)△ACN≌△MCB成立,CE=CF不成立.(答对一个得一分)
因为所有条件都没有发生改变,即
由∠ACM=∠BCN=60°,AC=MC,BC=NC,
∴∠ACN=∠MCB
∴△ACN≌△MCB(SAS);
因为证明△CEN≌△CFB的条件不够,
则CE=CF不成立;
(4)∠AOB度数没有发生改变,∠AOB =120°;

如上图,由三角形的外角性质,
∴∠AOB=∠ONB+∠OBN,
∵∠ABM=∠ANC,
又∠ONB=∠ANC+∠CNB,∠OBN=∠CBN-∠ABM,
∴∠AOB=∠CNB+∠CBN=120°,
故答案为:120°

 口算能手系列答案
口算能手系列答案