题目内容
如图10，在梯形ABCD中，AD∥BC，AB
= DC=1，BD平分∠ABC，BD⊥CD.
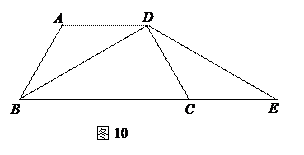
（1）求：① ∠BAD的度数；② BD的长；
（2）延长BC至点E，使C
E=CD，说明△DBE是等腰三角形
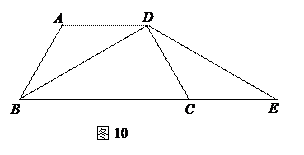
= DC=1，BD平分∠ABC，BD⊥CD.（1）求：① ∠BAD的度数；② BD的长；
（2）延长BC至点E，使C
E=CD，说明△DBE是等腰三角形（1）①120° ②
（2）证明略
（1）①∵ 梯形ABCD中，AD∥BC，AB= DC，
∴ ∠ABC=∠DCB，∠1=∠3，∠A+∠ABC=180°.
∵ BD平分∠ABC，
∴ ∠1=∠2，
∴ ∠1=∠2=∠3=
∠DCB.
∵ BD⊥CD，
（2） ∵ CE="CD" , ∴ ∠4=∠E=∠DCB=30°，
∵ ∠1=30°
∴ ∠1=∠E,
∴ DB="DE." 即△DBE是等腰三角形. ………………………………（12分）
∴ ∠ABC=∠DCB，∠1=∠3，∠A+∠ABC=180°.
∵ BD平分∠ABC，
∴ ∠1=∠2，
∴ ∠1=∠2=∠3=
∠DCB.∵ BD⊥CD，
（2） ∵ CE="CD" , ∴ ∠4=∠E=
∠DCB=30°，∵ ∠1=30°
∴ ∠1=∠E,
∴ DB="DE." 即△DBE是等腰三角形. ………………………………（12分）
练习册系列答案
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案
相关题目
是面积为4的正方形，函数
(
)的图象经过点
．
的值；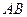
、
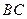翻折，得到正方形
、
．设线段
、
分别与函数
、
，求线段EF所在直线的解析式． 
中，
，
平分
，
交
于
.
是菱形；
的形状，并说明理由.
的值．
中，
为
的中点，连接
并延长交
的延长线于点
，则图中全等的直角三角形共有 （ ）
，
∥
，经测量知
cm，
cm，
，
，求梯形木料
：sin 67.4° = ，cos 67.4° = ，tan 67.4° = ）