题目内容
如图1,AD∥BC,AB ⊥BC于B,∠DCB=75°,以CD为边的等边△DCE的另一顶点E在线段AB上.

(1)填空:∠ADE=____°;
(2)求证: AB=BC;
(3)如图2所示,若F为线段CD上一点,∠FBC=30°,求 的值.
的值.

(1)填空:∠ADE=____°;
(2)求证: AB=BC;
(3)如图2所示,若F为线段CD上一点,∠FBC=30°,求
 的值.
的值.(1)45
(2)证明略
(3)1
解:(1)45; ……2分
(2)证明:连接AC
∵∠DCB=75º,AD∥BC
∴∠ADC="105º"
由等边△DCE可知:∠CDE =60º
故∠ADE =45º
由AB⊥BC,AD∥BC可得:∠DAB="90º"
∴∠AED=45º
∴AD="AE "
∴点A在线段DE的垂直平分线上 ……4分
又CD=CE
∴点C也在线段DE的垂直平分线上 ……5分
∴AC就是线段DE的垂直平分线
即AC⊥DE
∴AC平分∠EAD
∴∠BAC=45°
∴△ABC是等腰直角三角形
∴BA="BC " ……6分
(3)解:连接AF,延长BF交AD的延长线于点G
∵∠FBC=30º,∠ABC="90" º
∴∠ABF=60º,∠DCB=75º
∴∠BFC=75º
故BC=BF
由(2)知:BA=BC
∴BA=BF
∴△ABF是等边三角形
∴AB="BF=FA " ……7分
∴∠BAC="60" º
∴∠DAF="30" º
又∵AD∥BC
∴∠FAG=∠G=30º
∴FG ="FA=" FB ……8分
又∠DFG=∠CFB
∴△BCF≌△GDF(ASA) ……9分
∴DF=CF
∴="1 " ……10分
(2)证明:连接AC
∵∠DCB=75º,AD∥BC
∴∠ADC="105º"
由等边△DCE可知:∠CDE =60º
故∠ADE =45º
由AB⊥BC,AD∥BC可得:∠DAB="90º"
∴∠AED=45º
∴AD="AE "
∴点A在线段DE的垂直平分线上 ……4分
又CD=CE
∴点C也在线段DE的垂直平分线上 ……5分
∴AC就是线段DE的垂直平分线
即AC⊥DE
∴AC平分∠EAD
∴∠BAC=45°
∴△ABC是等腰直角三角形
∴BA="BC " ……6分
(3)解:连接AF,延长BF交AD的延长线于点G
∵∠FBC=30º,∠ABC="90" º
∴∠ABF=60º,∠DCB=75º
∴∠BFC=75º
故BC=BF
由(2)知:BA=BC
∴BA=BF
∴△ABF是等边三角形
∴AB="BF=FA " ……7分
∴∠BAC="60" º
∴∠DAF="30" º
又∵AD∥BC
∴∠FAG=∠G=30º
∴FG ="FA=" FB ……8分
又∠DFG=∠CFB
∴△BCF≌△GDF(ASA) ……9分
∴DF=CF
∴="1 " ……10分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,∠A=60°,E为
,∠A=60°,E为 边上的点,过点E作EF∥BD交AD于点F.将菱形先沿EF按图1所示方式折叠,点A落在点
边上的点,过点E作EF∥BD交AD于点F.将菱形先沿EF按图1所示方式折叠,点A落在点 处,过点
处,过点 处,
处,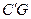 与
与 与
与 于点M、N.若点
于点M、N.若点 (即图中阴影部分)为“重叠四边形”.
(即图中阴影部分)为“重叠四边形”.




 ,若重叠四边形
,若重叠四边形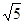 -1)cm B、
-1)cm B、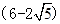 cm
cm 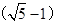 cm D、
cm D、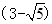 cm
cm
 = DC=1,BD平分∠ABC,BD⊥CD.
= DC=1,BD平分∠ABC,BD⊥CD.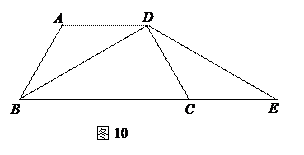
 E=CD,说明△DBE是等腰三角形
E=CD,说明△DBE是等腰三角形 的网格,网格中每个小正方形的边长均为1,每个网格中各画有一个梯形.请在图1、图2中分别画出一条线段,同时满足以下要求:
的网格,网格中每个小正方形的边长均为1,每个网格中各画有一个梯形.请在图1、图2中分别画出一条线段,同时满足以下要求:
 的坡度
的坡度 1:3,坝高
1:3,坝高 为2米,则斜坡
为2米,则斜坡



