Question

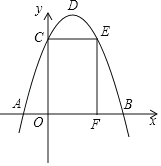
【题目】在平面直角坐标系xOy中,抛物线y=mx2－2mx +m－4 (m≠0)的顶点为A,与x轴交于B,C两点(B在点C左侧)，与y轴交于点D.

(1)求点A的坐标;

(2)若BC=4,

①求抛物线的解析式;

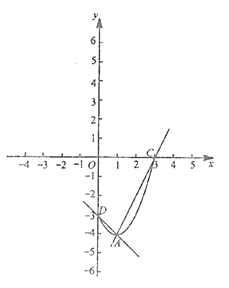
②将抛物线在C,D之间的部分记为图象G (包含C,D两点) . 若过点A的直线y= kx+ b(k≠0)与图象G有两个交点，结合函数的图象，求k的取值范围.

Answer 1

【答案】（1）(1,－4)；（2）①y= x2－2x－3；②-1≤k<0或0<k≤2

【解析】

（1）把一般式配成顶点式，即可得到A点坐标；

（2）根据对称轴，先求出点B、C的坐标，然后利用待定系数法，即可求出解析式；

②先求出点D（0，-3），画出抛物线，通过画图可得当k＞0时，直线y=kx+b过A、C时，k最大；当k＜0，直线y=kx+b过A、D时，k最大，然后分别求出两直线解析式，即可得到k的范围．

解：（1）y=mx2－2mx +m－4

=m(x2－2x+1)－4

=m(x－1)2－4.

∴点A的坐标为(1，－4) .；

（2）①由(1)得，抛物线的对称轴为：x= 1.

∵抛物线与x轴交于B，C两点(点B在点C左侧)，BC=4，

∴点B的坐标为(－1,0)，点C的坐标为(3，0) .

∴m+ 2m +m－4=0

∴m=1.

∴抛物线的解析式为：y= x2－2x－3；

②由①可得点D的坐标为：(0，－3).

当直线过点A， D时，解得：k=－1.

当直线过点A， C时，解得：k=2.

结合函数的图象可知，k的取值范围为：－1≤k<0或0<k≤2.