题目内容
【题目】下表是某次篮球联赛积分表的一部分:
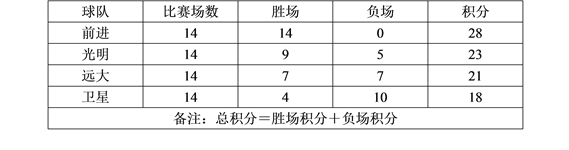
(1) 请问胜一场积多少分?负一场积多少分?(直接写出答案)
(2) 某队的胜场总积分能否等于负场总积分的3倍?为什么?
(3) 若某队的负场总积分是胜场总积分的n倍,n为正整数,试求n的值.
【答案】(1)胜一场2分,负一场1分;(2)不能;(3)n=3.
【解析】试题分析:(1)设胜一场积x分,则由前进队胜、负积分可知负一场积![]() 分,根据光明队胜9场负5场积23分即可得出关于x的一元一次方程,解之即可得出结论;
分,根据光明队胜9场负5场积23分即可得出关于x的一元一次方程,解之即可得出结论;
(2)设胜了x场,则负了(14﹣x)场,由胜一场积2分负一场积1分结合负场总积分是胜场总积分的3倍即可得出关于x的一元一次方程,解方程求出x值,再根据x为正整数判断结论的合理性;
(3)设胜了x场,则负了(14﹣x)场,由胜一场积2分负一场积1分结合负场总积分是胜场总积分的n倍即可得出关于x的一元一次方程,解方程求出x值,再根据x、n均为正整数即可得出n的值.
试题解析:解:(1)设胜一场积x分,则由前进队胜、负积分可知负一场积![]() 分,由光明队胜、负积分可得如下方程:
分,由光明队胜、负积分可得如下方程:
9x+![]() =23,解得:x=2,
=23,解得:x=2, ![]() =
=![]() =1.
=1.
答:胜一场积2分,负一场积1分.
(2)不能.理由如下:
设胜了x场,则负了(14﹣x)场,由题意得:
2x=3(14﹣x),解得:x=8.4.
∵x是正整数,∴某队的胜场总积分不能等于负场总积分的3倍;
(3)设胜了x场,则负了(14﹣x)场,由题意得:2nx=14﹣x,解得:x=![]() ,∵x和n均为正整数,∴2n+1为正奇数且又是14的约数,∴2n+1=7,∴n=3.
,∵x和n均为正整数,∴2n+1为正奇数且又是14的约数,∴2n+1=7,∴n=3.
答:n的值为3.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目