��Ŀ����
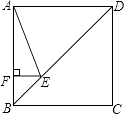
����Ŀ����ͼ����������A��B��C��������A��B��C��Ӧ�����ֱ���a��b��c��������![]() ��
��![]() ����c��10��2��0������P��A��������ÿ��1����λ���ٶ����յ�C�˶������˶�ʱ��Ϊt����
����c��10��2��0������P��A��������ÿ��1����λ���ٶ����յ�C�˶������˶�ʱ��Ϊt����
��1����a��b��c��ֵ��
��2������P��A��ľ����ǵ�P��B��ľ����2�������P��Ӧ������
��3������P�˶���B��ʱ����Q�ӵ�A��������ÿ��3����λ���ٶ���C���˶���Q�㵽��C�������������ͬ�����ٶȷ������˶����յ�A���ڵ�Q��ʼ�˶���ڼ���ʱ��P��Q����֮��ľ���Ϊ4����˵��������
���𰸡���1��a����24��b����10��c��10����2��t=28��![]() ����3���ڵ�Q��ʼ�˶����5��9��l2.5��14.5��ʱ��P��Q����֮��ľ�����4��
����3���ڵ�Q��ʼ�˶����5��9��l2.5��14.5��ʱ��P��Q����֮��ľ�����4��
�������������������1�����ݾ���ֵ��ż���ݾ��зǸ��Կɵ�a+24=0��b+10=0��c��10=0����ɵ�a��b��c��ֵ��
��2���ֱ��ʾ��P���Ӧ������AP��BP�ij����з��̼�����õ�P��Ӧ������
��3���������ۣ���P����Q����Ҳ࣬��Q�㻹û��P��ʱ����P��Q�����ʱ����Q����P���Q�㵽��C���P����Q�����ʱ����Q�㵽��C���P����Q���Ҳ�ʱ�����������ľ�����4���ɵ÷��̣����ݽⷽ�̣��ɵô𰸣�
����������⣺��1����|a+24|+|b+10|+��c��10��2=0����a+24=0��b+10=0��c��10=0����ã�a=��24��b=��10��c=10��
��2����P��A����1����λÿ����C�˶�����P����24��t����AP��t��BP��![]() ��
��
��t��2![]() ��t=28��
��t=28��![]() ��
��
��3����P����Q����Ҳ࣬��Q�㻹û��P��ʱ��3t+4=14+t�����t=5��
��P����Q�����ʱ����Q����P���3t��4=14+t�����t=9��
��Q�㵽��C���P����Q�����ʱ��14+t+4+3t��34=34��t=12.5��
��Q�㵽��C���P����Q���Ҳ�ʱ��14+t��4+3t��34=34�����t=14.5��������������Q�㿪ʼ�˶���5��9��12.5��14.5��ʱ��P��Q����֮��ľ���Ϊ4��