题目内容
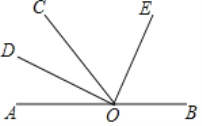
【题目】如图,∠AOB的平分线为OM,ON为∠MOA内的一条射线,OG为∠AOB外的一条射线.试说明:
(1)∠MON=![]() (∠BON-∠AON);
(∠BON-∠AON);
(2)∠MOG=![]() (∠AOG+∠BOG).
(∠AOG+∠BOG).

【答案】(1)证明见解析;(2)证明见解析.
【解析】根据角平分线定义和角的和差关系,得
(1)∠BON-∠AON=∠BOM+∠MON-∠AON=(∠BOM-∠AON)+∠MON=∠MON+∠MON=2∠MON;
(2)∠AOG+∠BOG=∠AOB+∠BOG+∠BOG=2∠MOB+2∠BOG=2(∠MOB+∠BOG)=2∠MOG.
解:(1)因为,∠BON=∠BOM+∠MON,
∠BON-∠AON
=∠BOM+∠MON-∠AON
=(∠BOM-∠AON)+ ∠MON
=∠MON+∠MON
=2∠MON,
所以,∠MON=![]() (∠BON-∠AON);
(∠BON-∠AON);
(2)因为,∠AOG+∠BOG
=∠AOB+∠BOG+∠BOG
=2∠MOB+2∠BOG
=2(∠MOB+∠BOG)
=2∠MOG,
所以,∠MOG=![]() (∠AOG+∠BOG).
(∠AOG+∠BOG).

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目