Question

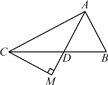
【题目】如图，在△ABC中，AD是∠BAC的平分线，且∠B＝∠ADB，过点C作CM垂直于AD的延长线，垂足为M.

(1)若∠DCM＝α，试用α表示∠BAD；

(2)求证：AB＋AC＝2AM.

Answer 1

【答案】（1）∠BAD＝2α；（2）证明见解析.

【解析】试题分析：(1)、根据垂直得出∠CDM=∠ADB=90°－α，然后根据∠BAD=180°－2∠ADB得出答案；(2)、延长AM到F使MF＝AM，连结CF，根据AD为角平分线得出∠CAF＝∠BAF＝∠F，根据平行线的性质得出∠FCD＝∠B＝∠ADB＝∠CDF，从而得出CF=DF，即AC=DF，从而得出答案．

试题解析：(1)、∵CM⊥AM，∠DCM＝α，∴∠CDM＝∠ADB＝∠B＝90°－α，

∴∠BAD＝180°－2∠ADB＝180°－2(90°－α)＝2α．

(2)、证明：延长AM到F使MF＝AM，连结CF，则有AC＝CF，

∵AD平∠BAC，∴∠CAF＝∠BAF＝∠F，∴CF∥AB， ∴∠FCD＝∠B＝∠ADB＝∠CDF，

∴CF＝DF，∴AC＝DF， ∵AD＋DF＝2AM，∴AB＋AC＝2AM．