题目内容
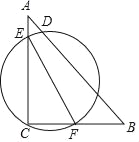
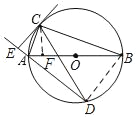
【题目】如图,⊙O是△ABC的外接圆,AB为直径,D是⊙O上一点,且弧CB=弧CD,CE⊥DA交DA的延长线于点E.
(1)求证:∠CAB=∠CAE;
(2)求证:CE是⊙O的切线;
(3)若AE=1,BD=4,求⊙O的半径长.

【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)连接BD,根据圆内接四边形的性质和等弧所对的圆周角相等,可得∠CAB=∠CAE;
(2)连接OC,由题意可得∠ACB=90°=∠AEC,即可证∠BCO=∠ACE=∠ABC,可得∠ECO=∠ACB=90°,则可证CE是⊙O的切线;
(3)过点C作CF⊥AB于点F,由角平分线的性质可得CE=CF,可证△CED≌△CFB,可得DE=BF,根据勾股定理可求⊙O的半径长.
证明:(1)连接BD
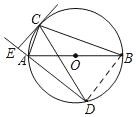
∵弧CB=弧CD,
∴∠CDB=∠CBD,CD=BC
∵四边形ACBD是圆内接四边形
∴∠CAE=∠CBD,且∠CAB=∠CDB,
∴∠CAB=∠CAE;
(2)连接OC
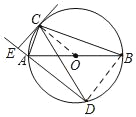
∵AB为直径,
∴∠ACB=90°=∠AEC,
又∵∠CAB=∠CAE,
∴∠ABC=∠ACE,
∵OB=OC,
∴∠BCO=∠CBO,
∴∠BCO=∠ACE,
∴∠ECO=∠ACE+∠ACO=∠BCO+∠ACO=∠ACB=90°,
∴EC⊥OC,
∵OC是⊙O的半径,
∴CE是⊙O的切线.
(3)过点C作CF⊥AB于点F,
又∵∠CAB=∠CAE,CE⊥DA,
∴AE=AF,
在△CED和△CFB中,
∵∠DEC=∠BFC=90°,
∠EDC=∠BFC,
CD=BC,
∴△CED≌△CFB(AAS),
∴ED=FB,
设AB=x,则AD=x﹣2,
在△ABD中,由勾股定理得,x2=(x﹣2)2+42,
解得,x=5,
∴⊙O的半径的长为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目