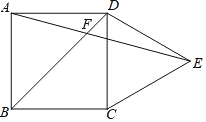
题目内容
【题目】如图，
、
是
的切线，切点分别为
、
，
是的直径，
与
相交于点
，连接
.下列结论：①
；②
；③若
，则
；④
.其中正确的个数为（ ）
A. 4个B. 3个C. 2个D. 1个
【答案】A
【解析】
本题先利用切线的性质，得到角的关系，再利用相似比求边的关系.
连接OB
∵
、
是
的切线，
∴PA⊥OA,PB⊥OB，AP=BP
又∵在Rt△APO与Rt△BPO中，OA=OB，OP=OP
∴Rt△APO≌Rt△BPO
∴∠APO=∠BPO
∴AB⊥OP
∵∠CAB+∠AOP=90°
∠APO+∠AOP=90°
∴∠CAB=∠APO
∴∠CAB=∠APO=∠BPO
∴
故①正确.
又∵AC是直径，∠ABC=90°
AB⊥OP
∴
故②正确.
∵tanC=3
∴
∴AB=3BC
∵OP⊥AB
∴
∵OA=OC
∴
∵OP⊥AB
∴∠ADO=∠ADP=90°
∵∠BAC=∠APO
∴△AOD∽△PAD
∴
∴AD2=OD·DP
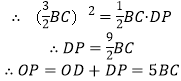
故③正确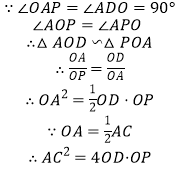
故④正确
故选A
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
