题目内容
【题目】如图，在平面直角坐标系中，直线y=﹣x+4与x轴、y轴分别交于点A、B．抛物线y=﹣ 
+n的顶点P在直线y=﹣x+4上，与y轴交于点C（点P、C不与点B重合），以BC为边作矩形BCDE，且CD=2，点P、D在y轴的同侧．
（1）n=（用含m的代数式表示），点C的纵坐标是（用含m的代数式表示）．
（2）当点P在矩形BCDE的边DE上，且在第一象限时，求抛物线对应的函数表达式．
（3）设矩形BCDE的周长为d（d＞0），求d与m之间的函数表达式．
（4）直接写出矩形BCDE有两个顶点落在抛物线上时m的值．
【答案】
（1）﹣m+4；﹣ 
m2﹣m+4
（2）
解：∵四边形BCDE是矩形，
∴DE∥y轴．
∵CD=2，
∴当x=2时，y=2．
∴DE与AB的交点坐标为（2，2）．
∴当点P在矩形BCDE的边DE上时，抛物线的顶点P坐标为（2，2）．
∴抛物线对应的函数表达式为 
（3）
解：∵直线y=﹣x+4与y轴交于点B，
∴点B的坐标是（0，4）．
当点B与点C重合时， 
．
解得m1=0，m2=﹣3．
i）当m＜﹣3或m＞0时，如图①、②， 
． 
．
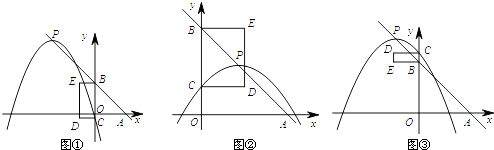
ii）当﹣3＜m＜0时，如图③， 
． 
（4）
解：如图④⑤，点C、D在抛物线上时，由CD=2可知对称轴为：x=±1，即m=±1；
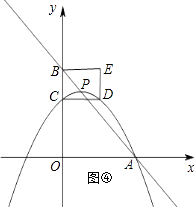
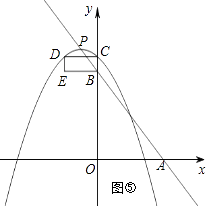
如图⑥⑦，点C、E在抛物线上时，由B（0，4）和CD=2得：E（﹣2，4）
则4=﹣ （﹣2﹣m）2+（﹣m+4），解得： 
、 
．
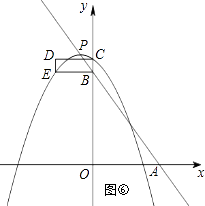
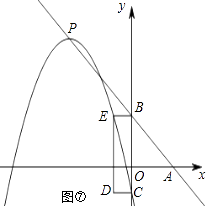
综上所述：m=1、m=﹣1、 、 ．
【解析】解：（1）y=﹣ （x﹣m）2+n=﹣ x2+ 
mx﹣ m2+n，
∴P（m，n），
∵点P在直线y=﹣x+4上，
∴n=﹣m+4，
当x=0时，y=﹣ m2+n=﹣ m2﹣m+4，
即点C的纵坐标为：﹣ m2﹣m+4，
所以答案是：﹣m+4，﹣ m2﹣m+4；
