题目内容
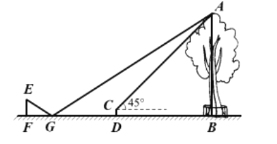
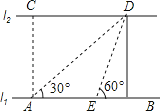
【题目】如图，河的两岸l1与l2互相平行，A、B是l1上的两点，C、D是l2上的两点，某同学在A处测得∠CAB＝90°，∠DAB＝30°，再沿AB方向走20米到达点E（即AE＝20），测得∠DEB＝60°.求：C，D两点间的距离.
【答案】30米
【解析】
过点D作DF⊥l1于点F，首先证明AE＝DE＝20，在Rt△DEF中，求出EF即可解决问题.
解：过点D作DF⊥l1于点F.
∵l1∥l2，∠CAB＝90°，
∴四边形CAFD是矩形，CD＝AF，
∵∠DAB＝30°，∠DEB＝60°，
∴∠ADE＝∠DEB﹣∠DAB＝30°，即∠ADE＝∠DAE，
∴AE＝DE＝20米，
在Rt△DEF中，∠DFE＝90°，∠DEF＝60°，DE＝20米，
∴EF＝10米，
∴CD＝AF＝AE+EF＝30米，
答：C，D两点间的距离是30米.
练习册系列答案
一本好题口算题卡系列答案
相关题目
【题目】小亮在研究矩形的面积S与矩形的边长x，y之间的关系时，得到下表数据：
x | 0.5 | 1 | 1.5 | 2 | 3 | 4 | 6 | 12 |
y | 12 | 6 | ■ | 3 | 2 | 1.5 | 1 | 0.5 |
结果发现一个数据被墨水涂黑了．
（1）被墨水涂黑的数据为_________；
（2）y与x的函数关系式为_________，且y随x的增大而_________；
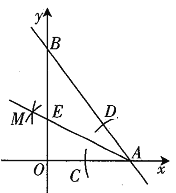
（3）如图是小亮画出的y关于x的函数图象，点B、E均在该函数的图象上，其中矩形
的面积记为
，矩形
的面积记为
，请判断与的大小关系，并说明理由；
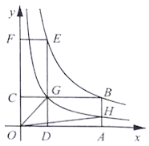
（4）在（3）的条件下，
交
于点G，反比例函数
的图象经过点G交
于点H，连接
、
，则四边形
的面积为_________．
