题目内容
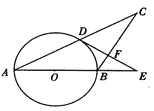
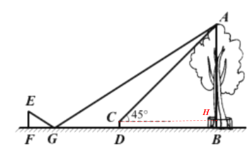
【题目】小明利用刚学过的测量知识来测量学校内一棵古树的高度。一天下午，他和学习小组的同学带着测量工具来到这棵古树前，由于有围栏保护，他们无法到达古树的底部B，如图所示。于是他们先在古树周围的空地上选择一点D，并在点D处安装了测量器DC，测得古树的顶端A的仰角为45°；再在BD的延长线上确定一点G，使DG=5米，并在G处的地面上水平放置了一个小平面镜，小明沿着BG方向移动，当移动带点F时，他刚好在小平面镜内看到这棵古树的顶端A的像，此时，测得FG=2米，小明眼睛与地面的距离EF=1.6米，测倾器的高度CD=0.5米。已知点F、G、D、B在同一水平直线上，且EF、CD、AB均垂直于FB，求这棵古树的高度AB。（小平面镜的大小忽略不计）
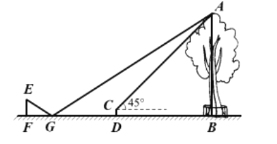
【答案】这棵古树的高AB为18m．
【解析】
如图，过点C作CH⊥AB于点H，则CH＝BD，BH＝CD＝0.5，继而可得AB＝BD＋0.5，再证明△EFG∽△ABC，根据相似三角形的性质得
，即
，由此求得BD长，即可求得AB长.
如图，过点C作CH⊥AB于点H，
则CH＝BD，BH＝CD＝0.5，
在Rt△ACH中，∠ACH＝45°，
∴AH＝CH＝BD，
∴AB＝AH＋BH＝BD＋0.5，
∵EF⊥FB，AB⊥FB，
∴∠EFG＝∠ABG＝90°，
由题意，易知∠EGF＝∠AGB，
∴△EFG∽△ABG，
∴，即，
解得：BD＝17.5，
∴AB=17.5＋0.5＝18(m)，
∴这棵古树的高AB为18m．
练习册系列答案
相关题目
