题目内容
【题目】如图,CD是⊙O的直径,OB⊥CD交⊙O于点B,连接CB,AB是⊙O的弦,AB交CD于点E,F是CD的延长线上一点且AF=EF.

(1)判断AF和⊙O的位置关系并说明理由.
(2)若∠ABC=60°,BC=1cm,求阴影部分的面积.(结果保留根号).
【答案】(1)AF和⊙O相切.理由见解析;(2)![]() cm2
cm2
【解析】
(1)连结OA,如图,由AF=AE得∠FAE=∠FEA,再利用对顶角相等和∠OBA=∠OAB可得∠OAB+∠FEA=90°,即∠OAF=90°,则OA⊥AF,然后根据切线的判定定理可判断AF为⊙O的切线;
(2)先判断△OBC为等腰直角三角形得到OB的长,再利用圆周角定理得到∠AOC=2∠ABC=120°,则∠AOF=180°-∠AOC=60°,接着根据正切定义计算得到AF,然后根据三角形面积公式和扇形面积公式,利用S阴影部分=S△OAF-S扇形AOD进行计算.
解:(1)AF和⊙O相切.
理由如下:
连结OA,
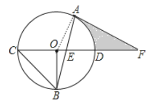
∵AF=AE,∴∠FAE=∠FEA,∵∠FEA=∠OEB,∴∠FAE=∠OEB,
∵OB⊥CD,∴∠BOE=90°,∴∠OBE+∠OEB=90°,
而OB=OA,∴∠OBA=∠OAB,
∴∠OAB+∠FEA=90°,即∠OAF=90°,
∴OA⊥AF,∴AF为⊙O的切线;
(2)∵OB⊥CD,而OB=OC,∴△OBC为等腰直角三角形,∴OB= BC=![]() ,
,
∵∠AOC=2∠ABC=2×60°=120°,∴∠AOF=180°-∠AOC=60°,
在Rt△OAF中,∵tan∠AOF=AF/AO,
∴AF=![]() ,
,
∴S阴影部分=S△OAF-S扇形AOD
=![]() ×
×![]() ×
×![]() -
-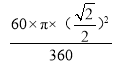
=![]() (cm2)
(cm2)

练习册系列答案
相关题目